Angular Size
Conversion between absolute and angular size units
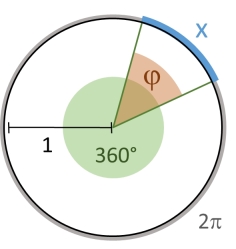
As mentioned in Describing Precision, group size is often measured in terms of its angular diameter in addition to reporting absolute length. Angles can be measured equivalently either in degree or in radian. If \(x\) is the angular measurement in radian, and \(\varphi\) the angular measurement in degree for the same angle, then \(\frac{x}{2 \pi} = \frac{\varphi}{360}\) such that conversion between degree and radian is given by \(x = \frac{2 \pi}{360} \cdot \varphi\) and \(\varphi = \frac{360}{2 \pi} \cdot x\).
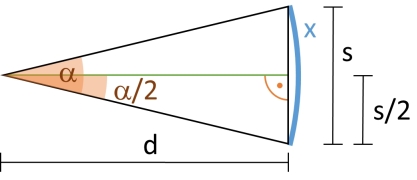
The angular size of an object with absolute size \(s\) is its angular diameter at a given distance \(d\). This is the angle \(\alpha\) subtended by the object with the line of sight centered on it. The following sections show how to convert between absolute size and these common units for angular size:
- MOA = minute of angle = minute of arc = arcmin. The circle is divided into 360 degrees, 1 MOA = 1/60 degree, such that the circle has \(360 \cdot 60 = 21600\) MOA.
- SMOA = Shooter's MOA = Inches Per Hundred Yards IPHY. 1 inch at 100 yards = 1 SMOA.
- milrad = milliradian = 1/1000 radian. 1 radian is 1 unit of arc length on the unit circle which has a circumference of \(2 \pi\). The circle is thus divided into \(2 \pi \cdot 1000 \approx 6283.19\) milrad.
Calculating the angular diameter of an object
The angle \(\alpha\) subtended by an object of size \(s\) at distance \(d\) can be calculated from the right triangle with hypotenuse of length \(d\) and cathetus of length \(s/2\) as \(\tan\left(\frac{\alpha}{2}\right) = \frac{s}{2} \cdot \frac{1}{d}\), therefore \(\alpha = 2 \cdot \arctan\left(\frac{s}{2 d}\right)\).
Assuming that the result from functions \(\tan(\cdot)\) and \(\arctan(\cdot)\) is in radian, and that distance to target \(d\) and object size \(s\) are measured in the same unit, this leads to the following formulas for calculating \(\alpha\) and \(x\) in milrad based on \(d\) and \(s\):
- Angle \(\alpha\) in MOA\[\alpha = 60 \cdot \frac{360}{2 \pi} \cdot 2 \cdot \arctan\left(\frac{s}{2 d}\right) = \frac{21600}{\pi} \cdot \arctan\left(\frac{s}{2 d}\right)\]
- Angle \(\alpha\) in SMOA: By definition, size \(s=1\) inch at \(d=100\) yards (\(= 3600\) inch) is 1 SMOA. Conversion factors to/from MOA are \(\frac{21600}{\pi} \cdot \arctan\left(\frac{1}{2 \cdot 3600}\right) \approx 0.95493\) (fairly close to \(3/\pi\)), and \(\frac{\pi}{21600} \cdot \frac{1}{\arctan(1/7200)} \approx 1.04720\) (fairly close to \(\pi/3\)). Therefore\[\alpha = \frac{\pi}{21600} \cdot \frac{1}{\arctan(1/7200)} \cdot \frac{21600}{\pi} \cdot \arctan\left(\frac{s}{2 d}\right) = \frac{1}{\arctan(1/7200)} \cdot \arctan\left(\frac{s}{2 d}\right)\]
- Arc length \(x\) in milrad\[x = 1000 \cdot 2 \cdot \arctan\left(\frac{s}{2 d}\right) = 2000 \cdot \arctan\left(\frac{s}{2 d}\right)\]
(Conversion from MOA to mils is \(\frac{21600}{2000 \pi} \approx 3.43775\). Conversion from mils to MOA is \(\frac{2000 \pi}{21600} \approx 0.29089\).)
We can also give formulas for object size \(s\) given angle \(\alpha\) and distance to target \(d\):
- From angle \(\alpha\) in MOA\[s = 2 \cdot d \cdot \tan\left( \frac{(2 \pi/360) (\alpha / 60)}{2} \right) = 2 \cdot d \cdot \tan\left(\alpha \cdot \frac{\pi}{21600}\right)\]
- From angle \(\alpha\) in SMOA\[s = \frac{21600}{\pi} \cdot \arctan\left(\frac{1}{7200}\right) \cdot 2 \cdot d \cdot \tan\left(\alpha \cdot \frac{\pi}{21600}\right)\]
- From arc length \(x\) in milrad\[s = 2 \cdot d \cdot \tan\left(\frac{x/1000}{2}\right) = 2 \cdot d \cdot \tan(0.0005 x)\]
Less accurate calculation of angular size
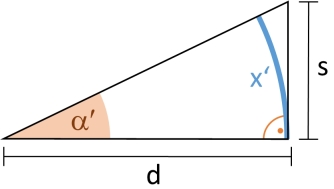
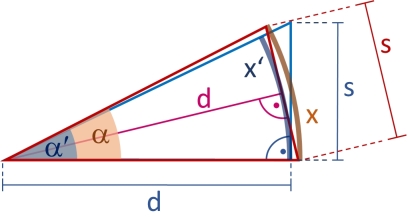
Sometimes, a slightly different angular size is reported as corresponding to absolute size \(s\) at distance \(d\): This is the angle \(\alpha'\) subtended by the object if it "sits" on the line of sight. \(\alpha'\) can be calculated from the right triangle with hypotenuse of length \(d\) and cathetus of length \(s\), so \(\tan(\alpha') = \frac{s}{d}\), therefore \(\alpha' = \arctan(\frac{s}{d})\).
If size \(s\) is small compared to distance \(d\), the difference between the actual angular diameter \(\alpha\) and the approximate angular size \(\alpha'\) is negligible, but it becomes noticeable once \(s\) gets bigger in relation to \(d\).