Difference between revisions of "Closed Form Precision"
| Line 17: | Line 17: | ||
:<math>CEP_n = \sigma \frac{\sqrt{\ln(4)}}{c_{G}(n) c_{R}(n)}</math> | :<math>CEP_n = \sigma \frac{\sqrt{\ln(4)}}{c_{G}(n) c_{R}(n)}</math> | ||
| − | The three measures that vary with ''n'' are range statistics without convenient functional forms. However both the mean and standard deviation of their expected value scales with ''σ'', so it is sufficient to calculate them once for ''σ'' = 1 and multiply the resulting values by the actual ''σ''. [[ | + | The three measures that vary with ''n'' are range statistics without convenient functional forms. However both the mean and standard deviation of their expected value scales with ''σ'', so it is sufficient to calculate them once for ''σ'' = 1 and multiply the resulting values by the actual ''σ''. [[Media:Sigma1ShotStatistics.ods]] contains those values for ''n'' up to 100. |
Revision as of 22:48, 19 November 2013
Measuring Precision showed how a single parameter σ characterizes the precision of a shooting system.
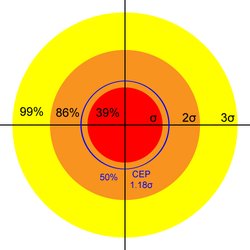
This σ is the parameter for the Rayleigh distribution with probability density function \(\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}\). The associated Cumulative Distribution Function gives us the probability that a shot falls within a given radius of the center: \[Pr(r \leq \alpha) = 1 - e^{-\alpha^2 / 2 \sigma}\] Therefore, we expect 39% of shots to fall within a circle of radius σ, 86% within 2σ, and 99% within 3σ.
Using the characteristics of the Rayleigh distribution we can immediately compute the three most useful precision measures:
Radial Standard Deviation \(RSD = \sigma \sqrt{2}\). The expected sample RSD of a group of size n is \[RSD_n = \sigma \sqrt{\frac{2}{c_{G}(n)}} \approx \sigma \sqrt{2 - \frac{1}{2n} - \frac{7}{16n^2} - \frac{19}{64n^3}}\]
Mean Radius \(MR = \sigma \sqrt{\frac{\pi}{2}}\). The expected sample MR of a group of size n is \[MR_n = \sigma \sqrt{\frac{\pi}{2 c_{B}(n)}}\ = \sigma \sqrt{\frac{\pi (n - 1)}{2 n}}\]
Circular Error Probable \(CEP = \sigma \sqrt{\ln(4)}\). The expected sample CEP of a group of size n is \[CEP_n = \sigma \frac{\sqrt{\ln(4)}}{c_{G}(n) c_{R}(n)}\]
The three measures that vary with n are range statistics without convenient functional forms. However both the mean and standard deviation of their expected value scales with σ, so it is sufficient to calculate them once for σ = 1 and multiply the resulting values by the actual σ. Media:Sigma1ShotStatistics.ods contains those values for n up to 100.