Difference between revisions of "Closed Form Precision"
m |
|||
| Line 1: | Line 1: | ||
| + | = The Precision Parameter = | ||
[[Measuring Precision]] showed how a single parameter ''σ'' characterizes the precision of a shooting system. | [[Measuring Precision]] showed how a single parameter ''σ'' characterizes the precision of a shooting system. | ||
[[File:RayleighProcess.png|250px|thumb|right|Rayleigh Probabilities|Rayleigh distribution of shots given ''σ'']] | [[File:RayleighProcess.png|250px|thumb|right|Rayleigh Probabilities|Rayleigh distribution of shots given ''σ'']] | ||
This ''σ'' is the parameter for the Rayleigh distribution with probability density function <math>\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}</math>. The associated Cumulative Distribution Function gives us the probability that a shot falls within a given radius of the center: | This ''σ'' is the parameter for the Rayleigh distribution with probability density function <math>\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}</math>. The associated Cumulative Distribution Function gives us the probability that a shot falls within a given radius of the center: | ||
| − | :<math>Pr(r \leq \alpha) = 1 - e^{-\alpha^2 / 2 \sigma}</math> | + | : <math>Pr(r \leq \alpha) = 1 - e^{-\alpha^2 / 2 \sigma}</math> |
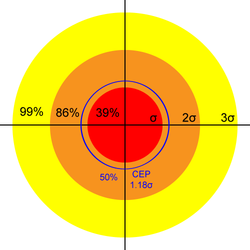
Therefore, we expect 39% of shots to fall within a circle of radius ''σ'', 86% within ''2σ'', and 99% within ''3σ''. | Therefore, we expect 39% of shots to fall within a circle of radius ''σ'', 86% within ''2σ'', and 99% within ''3σ''. | ||
Using the characteristics of the Rayleigh distribution we can immediately compute the three most useful [[Describing_Precision#Measures|precision measures]]: | Using the characteristics of the Rayleigh distribution we can immediately compute the three most useful [[Describing_Precision#Measures|precision measures]]: | ||
| + | == Radial Standard Deviation (RSD) == | ||
Radial Standard Deviation <math>RSD = \sigma \sqrt{2}</math>. The expected sample RSD of a group of size ''n'' is | Radial Standard Deviation <math>RSD = \sigma \sqrt{2}</math>. The expected sample RSD of a group of size ''n'' is | ||
| − | :<math>RSD_n = \sigma \sqrt{\frac{2}{c_{G}(n)}} \approx \sigma \sqrt{2 - \frac{1}{2n} - \frac{7}{16n^2} - \frac{19}{64n^3}}</math> | + | : <math>RSD_n = \sigma \sqrt{\frac{2}{c_{G}(n)}} \approx \sigma \sqrt{2 - \frac{1}{2n} - \frac{7}{16n^2} - \frac{19}{64n^3}}</math> |
| + | == Mean Radius (MR) == | ||
Mean Radius <math>MR = \sigma \sqrt{\frac{\pi}{2}}</math>. The expected sample MR of a group of size ''n'' is | Mean Radius <math>MR = \sigma \sqrt{\frac{\pi}{2}}</math>. The expected sample MR of a group of size ''n'' is | ||
| − | :<math>MR_n = \sigma \sqrt{\frac{\pi}{2 c_{B}(n)}}\ = \sigma \sqrt{\frac{\pi (n - 1)}{2 n}}</math> | + | : <math>MR_n = \sigma \sqrt{\frac{\pi}{2 c_{B}(n)}}\ = \sigma \sqrt{\frac{\pi (n - 1)}{2 n}}</math> |
| + | == Circular Error Probable (CEP) == | ||
Circular Error Probable <math>CEP = \sigma \sqrt{\ln(4)}</math>. The expected sample CEP of a group of size ''n'' is | Circular Error Probable <math>CEP = \sigma \sqrt{\ln(4)}</math>. The expected sample CEP of a group of size ''n'' is | ||
| − | :<math>CEP_n = \sigma \frac{\sqrt{\ln(4)}}{c_{G}(n) c_{R}(n)}</math> | + | : <math>CEP_n = \sigma \frac{\sqrt{\ln(4)}}{c_{G}(n) c_{R}(n)}</math> |
| + | == Spread Measures == | ||
The three measures that vary with ''n'' are range statistics that lack convenient functional forms. However both the mean and standard deviation of their expected value scales with ''σ'', so it is sufficient to calculate them once for ''σ'' = 1 and multiply the resulting values by the desired ''σ''. [[Media:Sigma1ShotStatistics.ods]] contains those values for ''n'' up to 100. | The three measures that vary with ''n'' are range statistics that lack convenient functional forms. However both the mean and standard deviation of their expected value scales with ''σ'', so it is sufficient to calculate them once for ''σ'' = 1 and multiply the resulting values by the desired ''σ''. [[Media:Sigma1ShotStatistics.ods]] contains those values for ''n'' up to 100. | ||
Revision as of 14:11, 20 November 2013
Contents
The Precision Parameter
Measuring Precision showed how a single parameter σ characterizes the precision of a shooting system.
This σ is the parameter for the Rayleigh distribution with probability density function \(\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}\). The associated Cumulative Distribution Function gives us the probability that a shot falls within a given radius of the center:
- \(Pr(r \leq \alpha) = 1 - e^{-\alpha^2 / 2 \sigma}\)
Therefore, we expect 39% of shots to fall within a circle of radius σ, 86% within 2σ, and 99% within 3σ.
Using the characteristics of the Rayleigh distribution we can immediately compute the three most useful precision measures:
Radial Standard Deviation (RSD)
Radial Standard Deviation \(RSD = \sigma \sqrt{2}\). The expected sample RSD of a group of size n is
- \(RSD_n = \sigma \sqrt{\frac{2}{c_{G}(n)}} \approx \sigma \sqrt{2 - \frac{1}{2n} - \frac{7}{16n^2} - \frac{19}{64n^3}}\)
Mean Radius (MR)
Mean Radius \(MR = \sigma \sqrt{\frac{\pi}{2}}\). The expected sample MR of a group of size n is
- \(MR_n = \sigma \sqrt{\frac{\pi}{2 c_{B}(n)}}\ = \sigma \sqrt{\frac{\pi (n - 1)}{2 n}}\)
Circular Error Probable (CEP)
Circular Error Probable \(CEP = \sigma \sqrt{\ln(4)}\). The expected sample CEP of a group of size n is
- \(CEP_n = \sigma \frac{\sqrt{\ln(4)}}{c_{G}(n) c_{R}(n)}\)
Spread Measures
The three measures that vary with n are range statistics that lack convenient functional forms. However both the mean and standard deviation of their expected value scales with σ, so it is sufficient to calculate them once for σ = 1 and multiply the resulting values by the desired σ. Media:Sigma1ShotStatistics.ods contains those values for n up to 100.