Closed Form Precision
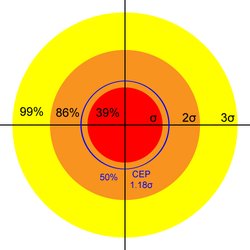
Measuring Precision showed how a single parameter σ characterizes the precision of a shooting system.
This σ is the parameter for the Rayleigh distribution with probability density function \(\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}\). The associated Cumulative Distribution Function gives us the probability that a shot falls within a given radius of the center: \[Pr(r \leq \alpha) = 1 - e^{-\alpha^2 / 2 \sigma}\] Therefore, we expect 39% of shots to fall within a circle of radius σ, 86% within 2σ, and 99% within 3σ.
Using the characteristics of the Rayleigh distribution we can immediately compute the three most useful precision measures:
Radial Standard Deviation \(RSD = \sigma \sqrt{2}\). The expected sample RSD of a group of size n is \[RSD_n = \sigma \sqrt{\frac{2}{c_{G}(n)}} \approx \sigma \sqrt{2 - \frac{1}{2n} - \frac{7}{16n^2} - \frac{19}{64n^3}}\]
Mean Radius \(MR = \sigma \sqrt{\frac{\pi}{2}}\). The expected sample MR of a group of size n is \[MR_n = \sigma \sqrt{\frac{\pi}{2 c_{B}(n)}}\ = \sigma \sqrt{\frac{\pi (n - 1)}{2 n}}\]
Circular Error Probable \(CEP = \sigma \sqrt{\ln(4)}\).