Closed Form Precision
Contents
The Precision Parameter
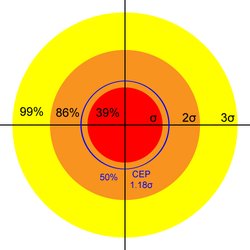
Measuring Precision showed how a single parameter σ characterizes the precision of a shooting system.
This σ is the parameter for the Rayleigh distribution with probability density function \(\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}\). The associated Cumulative Distribution Function gives us the probability that a shot falls within a given radius of the center:
- \(Pr(r \leq \alpha) = 1 - e^{-\alpha^2 / 2 \sigma}\)
Therefore, we expect 39% of shots to fall within a circle of radius σ, 86% within 2σ, and 99% within 3σ.
Using the characteristics of the Rayleigh distribution we can immediately compute the three most useful precision measures:
Radial Standard Deviation (RSD)
Radial Standard Deviation \(RSD = \sigma \sqrt{2}\). The expected sample RSD of a group of size n is
- \(RSD_n = \sigma \sqrt{\frac{2}{c_{G}(n)}} \approx \sigma \sqrt{2 - \frac{1}{2n} - \frac{7}{16n^2} - \frac{19}{64n^3}}\)
Mean Radius (MR)
Mean Radius \(MR = \sigma \sqrt{\frac{\pi}{2}}\). The expected sample MR of a group of size n is
- \(MR_n = \sigma \sqrt{\frac{\pi}{2 c_{B}(n)}}\ = \sigma \sqrt{\frac{\pi (n - 1)}{2 n}}\)
Circular Error Probable (CEP)
Circular Error Probable \(CEP = \sigma \sqrt{\ln(4)}\). The expected sample CEP of a group of size n is
- \(CEP_n = \sigma \frac{\sqrt{\ln(4)}}{c_{G}(n) c_{R}(n)}\)
Spread Measures
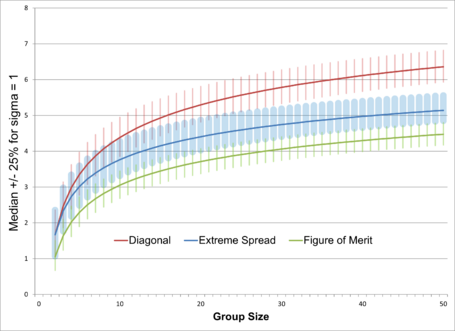
The three measures that vary with n (Extreme Spread, Diagonal, and Figure of Merit) are range statistics that lack convenient functional forms. However both the mean and standard deviation of their expected value, as well as quantiles, scale directly with σ, so it is sufficient to calculate those statistics once for σ = 1 and multiply the resulting values by the desired σ. Media:Sigma1RangeStatistics.xls contains quantiles and moments for n up to 100.
Example 1
The extreme spread median from the table for 5 shots is 3.0 σ. I've determined my rifle has precision σ = ½MOA. If I take five shots at 100 yards we would expect half my groups to be less than 3.0/2 = 1.5MOA \(\approx\) 1.6".
Multiplying the rest of the distribution data for that row by my 0.5MOA we can also say that the extreme spread of my 5-shot groups should exhibit the following distributions:
- 50% between (1.2, 1.8)MOA
- 80% between (1.0, 2.1)MOA
- 95% between (0.8, 2.4)MOA
Example 2
Over many tests I have found my rifle produces 5-shot groups with an average extreme spread of 1MOA. What extreme spread should I expect if I instead start shooting 10-shot groups? The table shows that the ratio of expected extreme spreads on 10-shot groups is 1.24 times the value on 5-shot groups. So my a priori expectation would be for 10-shot groups to average 1.24MOA.