Difference between revisions of "Describing Precision"
| Line 33: | Line 33: | ||
(There are some methods for dealing with the case of targets with [[ragged holes]] in which we can't determine the precise coordinates of each shot.) | (There are some methods for dealing with the case of targets with [[ragged holes]] in which we can't determine the precise coordinates of each shot.) | ||
| − | == Mean Radius == | + | == Mean Radius (MR) == |
: <math>\bar{R} = \sum_{}^n r_i / n</math> where <math>r_i = \sqrt{(x_i - \bar{x})^2 + (y_i - \bar{y})^2}</math> | : <math>\bar{R} = \sum_{}^n r_i / n</math> where <math>r_i = \sqrt{(x_i - \bar{x})^2 + (y_i - \bar{y})^2}</math> | ||
| − | As we will see in [[ | + | As we will see in [[Closed Form Precision]], the Mean Radius is typically only 6% larger than the Circular Error Probable. Since this is within the margin of error of most real-world usage the terms MR and CEP may be casually interchanged. |
== [[Circular Error Probable]] (CEP) == | == [[Circular Error Probable]] (CEP) == | ||
| Line 48: | Line 48: | ||
RSD has been given various definitions in the [[Prior Art]]. However, none of them are actually the standard deviation of radii <math>r_i</math>. When <math>\sigma_x \neq \sigma_y</math> the variance of radii has to be computed using <math>\frac{\sigma_x^2}{\pi} (\pi - 2 K^2(1 - \frac{\sigma_y^2}{\sigma_x^2})) + \sigma_y^2</math> where ''K'' is the complete elliptic integral. | RSD has been given various definitions in the [[Prior Art]]. However, none of them are actually the standard deviation of radii <math>r_i</math>. When <math>\sigma_x \neq \sigma_y</math> the variance of radii has to be computed using <math>\frac{\sigma_x^2}{\pi} (\pi - 2 K^2(1 - \frac{\sigma_y^2}{\sigma_x^2})) + \sigma_y^2</math> where ''K'' is the complete elliptic integral. | ||
| − | + | If we assume that <math>\sigma_x = \sigma_y</math> then, per the Rayleigh model described in [[Closed Form Precision]], we get the following simple formula: | |
: <math>RSD = \sigma \sqrt{\frac{4 - \pi}{2}}</math> | : <math>RSD = \sigma \sqrt{\frac{4 - \pi}{2}}</math> | ||
| Line 62: | Line 62: | ||
RC is the radius of the smallest circle containing all shot centers. This will either pass through the two extreme points -- in which case RC = (Extreme Spread) / 2 -- or else it will pass through three outside points. | RC is the radius of the smallest circle containing all shot centers. This will either pass through the two extreme points -- in which case RC = (Extreme Spread) / 2 -- or else it will pass through three outside points. | ||
| − | == | + | == Extreme Spread == |
| − | The | + | The Extreme Spread <math>ES = \max \sqrt{(x_i - x_j)^2 - (y_i - y_j)^2)}</math> is the largest distance between any two points, ''i'' and ''j'', in the group. |
= Which Measure is Best? = | = Which Measure is Best? = | ||
| Line 71: | Line 71: | ||
== Invariant Measures == | == Invariant Measures == | ||
* Mean Radius | * Mean Radius | ||
| − | * | + | * Circular Error Probable |
* Variance | * Variance | ||
* Standard Deviation | * Standard Deviation | ||
| Line 78: | Line 78: | ||
In fact we will see that when <math>\sigma_h = \sigma_v</math> each of these four measures is just a scalar function of ''σ'', so they all convey the same underlying information. | In fact we will see that when <math>\sigma_h = \sigma_v</math> each of these four measures is just a scalar function of ''σ'', so they all convey the same underlying information. | ||
| − | == Range Statistics == | + | == [[Range Statistics]] == |
| − | * | + | * Extreme Spread |
* Diagonal | * Diagonal | ||
* Figure of Merit | * Figure of Merit | ||
| Line 86: | Line 86: | ||
= Precision Guarantees = | = Precision Guarantees = | ||
| − | ''How meaningful is a 3-shot precision guarantee?'' The first answer is that ''any performance standard that is expressed in terms of | + | ''How meaningful is a 3-shot precision guarantee?'' The first answer is that ''any performance standard that is expressed in terms of Extreme Spread is probably meaningless''. After all, even the most precise gun will occasionally shoot a wide 3-shot group, and a shot-out barrel will with some probability still put three rounds through the same hole. The inherent precision of a gun is revealed over a large number of shots, and it doesn't matter how those shots are sampled: neither the gun nor the target has a memory. If we shoot 100 rounds through a rifle, we could pick any three at random as a 3-shot group. Therefore, a precision guarantee has to hold over a large number of shots and is more aptly expressed in terms of probabilities. E.g., "99% of shots with our rifle will fall within a ½MOA radius." As we will see in [[Closed Form Precision]] such a 99% claim is the same as saying 3''σ'' = ½MOA, or that the rifle's precision ''σ'' = 1/6MOA. Which is the same as saying [[Circular Error Probable]] = 0.2MOA. |
There are two qualifications to the preceding: | There are two qualifications to the preceding: | ||
Revision as of 13:38, 26 February 2014
Previous: What is Precision?
Units
When we talk about shooting precision we are referring to the amount of dispersion we expect to see of each shot about a center point (which shooters try to adjust to match the point of aim). Precision is like a cone of error that projects out from the muzzle of the gun. I.e., double the distance and the dispersion also doubles. We can describe this error by referring to dispersion at a specific distance. For example, it is common to quote precision in inches of extreme spread at 100 yards, or "inches per hundred yards."
It is more common, however, to describe Angular Size – i.e., the angle of the cone at its tip – since this is independent of the distance at which a target is shot. The higher the precision, the tighter the cone and the smaller the angle at its tip.
One of two popular angular units used by shooters is MOA, though there is some ambiguity in this term. MOA was initially short for Minute of Arc, or arc minute, which is one sixtieth of one degree. At 100 yards (3600 inches) one MOA is 3600" tan (1/60 degrees) = 1.047". At some point shooters began to expand the acronym as Minute of Angle. They also and rounded its correct value to 1” at 100 yards, though for clarity the latter unit is properly called "Shooters MOA," or SMOA.
The other common unit is the mil, which simply means thousandth. For example, at 100 yards a mil is 100 yards / 1000 = 3.6". Some more benign confusion also persists around this term, with some assuming "mil" is short for milliradian, which is another angular unit. Fortunately, a milliradian is almost exactly equal to a mil so there’s no harm interchanging mil, mrad, milrad, and milliradian.
NB: 1 mil = 3.6 SMOA \(\approx\) 3.44 MOA. See Angular Size for detailed illustrations and conversion formulas.
Examples
One of the important questions addressed here is what to measure in order to determine the intrinsic precision of a shooting system, and what sample size is sufficient to achieve any degree of statistical significance.
Following are common measurements used in the industry:
- Extreme Spread of a 3-shot group, usually at 100 yards. This is statistically almost meaningless, especially when there is no reference to how many 3-shot groups were sampled. (An extended practical, and amusing, critique of the 3-shot group is archived here.)
- Extreme Spread of a 5-shot group, sometimes excluding the worst shot. Hardly any better.
- Average, Max, and Min Extreme Spread of five 5-shot groups. (This is used by the NRA's magazines.)
- The US Army Marksmanship Unit at Ft. Benning, GA uses a minimum of 3 consecutive 10-shot groups fired with the rifle in a machine rest when testing service rifles. The military also often explicitly uses the more statistically powerful Mean Radius and Circular Error Probable measures.
Measures
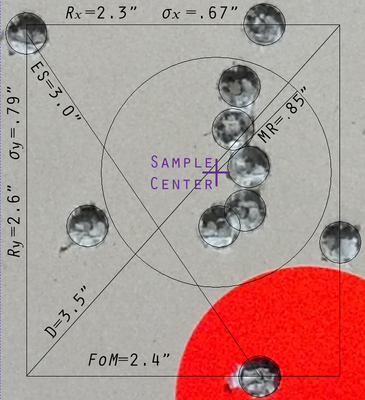
Eight different measures have been used to characterize the dispersion of bullet holes in a sample target. Some are easier to calculate than others.
In the following formulas assume that we are looking at a target reflecting n shots and that we are able to determine the center coordinates x and y for each shot.
As is customary, the mean value of a set of values \({x}\) is called "x-bar" and defined as \(\bar{x} \equiv \sum_{}^n x_i / n\).
(There are some methods for dealing with the case of targets with ragged holes in which we can't determine the precise coordinates of each shot.)
Mean Radius (MR)
- \(\bar{R} = \sum_{}^n r_i / n\) where \(r_i = \sqrt{(x_i - \bar{x})^2 + (y_i - \bar{y})^2}\)
As we will see in Closed Form Precision, the Mean Radius is typically only 6% larger than the Circular Error Probable. Since this is within the margin of error of most real-world usage the terms MR and CEP may be casually interchanged.
Circular Error Probable (CEP)
CEP(p), for \(p \in [0, 1)\), is the radius of the smallest circle that covers proportion p of the shot group. When p is not indicated it is assumed to be 50%, which is the median shot radius.
Horizontal and Vertical Variance
- \(\sigma_h^2 = \frac{\sum^{n}(x_i - \bar{x})^2}{n - 1}, \quad \sigma_v^2 = \frac{\sum^{n}(y_i - \bar{y})^2}{n - 1}\)
(Often these will be given as standard deviations, which is just the square root of variance.)
Radial Standard Deviation (RSD)
RSD has been given various definitions in the Prior Art. However, none of them are actually the standard deviation of radii \(r_i\). When \(\sigma_x \neq \sigma_y\) the variance of radii has to be computed using \(\frac{\sigma_x^2}{\pi} (\pi - 2 K^2(1 - \frac{\sigma_y^2}{\sigma_x^2})) + \sigma_y^2\) where K is the complete elliptic integral.
If we assume that \(\sigma_x = \sigma_y\) then, per the Rayleigh model described in Closed Form Precision, we get the following simple formula:
- \(RSD = \sigma \sqrt{\frac{4 - \pi}{2}}\)
Diagonal
Let \(\hat{X} = x_\max - x_\min, \quad \hat{Y} = y_\max - y_\min\) — i.e., the ranges of x and y values.
The diagonal \(D = \sqrt{\hat{X}^2 + \hat{Y}^2}\) is the length of the diagonal line through the smallest rectangle covering the sample group.
Figure of Merit
FoM = \((\hat{X} + \hat{Y}) / 2\) is the average extreme width and height of the group.
Radius of Covering Circle
RC is the radius of the smallest circle containing all shot centers. This will either pass through the two extreme points -- in which case RC = (Extreme Spread) / 2 -- or else it will pass through three outside points.
Extreme Spread
The Extreme Spread \(ES = \max \sqrt{(x_i - x_j)^2 - (y_i - y_j)^2)}\) is the largest distance between any two points, i and j, in the group.
Which Measure is Best?
Measuring Precision will detail the mathematical relationships between many of these measures.
Invariant Measures
- Mean Radius
- Circular Error Probable
- Variance
- Standard Deviation
It is worth noting that these first four measures do not vary with group size. I.e., taking more shots tightens their confidence interval but doesn't change their expected value.
In fact we will see that when \(\sigma_h = \sigma_v\) each of these four measures is just a scalar function of σ, so they all convey the same underlying information.
Range Statistics
- Extreme Spread
- Diagonal
- Figure of Merit
- Covering Circle Radius
These measures increase with group size. They are more commonly used because they are easier to calculate. But they are statistically far weaker because they virtually ignore inner data points.
Precision Guarantees
How meaningful is a 3-shot precision guarantee? The first answer is that any performance standard that is expressed in terms of Extreme Spread is probably meaningless. After all, even the most precise gun will occasionally shoot a wide 3-shot group, and a shot-out barrel will with some probability still put three rounds through the same hole. The inherent precision of a gun is revealed over a large number of shots, and it doesn't matter how those shots are sampled: neither the gun nor the target has a memory. If we shoot 100 rounds through a rifle, we could pick any three at random as a 3-shot group. Therefore, a precision guarantee has to hold over a large number of shots and is more aptly expressed in terms of probabilities. E.g., "99% of shots with our rifle will fall within a ½MOA radius." As we will see in Closed Form Precision such a 99% claim is the same as saying 3σ = ½MOA, or that the rifle's precision σ = 1/6MOA. Which is the same as saying Circular Error Probable = 0.2MOA.
There are two qualifications to the preceding:
- We do know that the sample size of a 3-shot group is smaller than the sample size of larger groups, simply because the sample center is almost certainly some distance from the true center. This effect is covered in the section on Correction Factors. For example, the average 3-shot group has a mean radius \(1/\sqrt{c_B(3)} \approx 80\%\) the size of the mean radius measured from twenty or more shots.
- It is not exactly true that guns have no memory: The effects of heating and fouling can create second-order changes in both the precision and point of impact. So it might be necessary to qualify a precision guarantee with limits on barrel temperature and/or prescriptions on how many shots be fired before and after bore cleaning. And in the limit barrels erode and have a finite lifespan, so especially with higher-power calibers practical limits do exist on how long precision can stay constant.
Next: Measuring Precision