Difference between revisions of "Describing Precision"
(→Units) |
m |
||
| Line 73: | Line 73: | ||
= Which Measure is Best? = | = Which Measure is Best? = | ||
| − | [[ | + | [[Precision Models]] will detail the mathematical relationships between many of these measures. |
== Invariant Measures == | == Invariant Measures == | ||
| Line 93: | Line 93: | ||
<BR/> | <BR/> | ||
<HR/> | <HR/> | ||
| − | <p style="text-align:right"><B>Next:</B> [[ | + | <p style="text-align:right"><B>Next:</B> [[Precision Models]]</p> |
Revision as of 16:10, 22 April 2015
Previous: What is Precision?
Units
When we talk about shooting precision we are referring to the amount of dispersion we expect to see of each shot about a center point (which shooters try to adjust to match the point of aim). Precision is like a cone of error that projects out from the muzzle of the gun. I.e., double the distance and the dispersion also doubles. We can describe this error by referring to dispersion at a specific distance. For example, it is common to quote precision in inches of extreme spread at 100 yards, or "inches per hundred yards" (IPHY).
It is more common, however, to describe Angular Size – i.e., the angle of the cone at its tip – since this is independent of the distance at which a target is shot. The higher the precision, the tighter the cone and the smaller the angle at its tip.
One of two popular angular units used by shooters is MOA, though there is some ambiguity in this term. MOA was initially short for Minute of Arc, or arc minute, which is one sixtieth of one degree. At 100 yards (3600 inches) one MOA is 3600" tan (1/60 degrees) = 1.047". At some point shooters began to expand the acronym as Minute of Angle. They also and rounded its correct value to 1” at 100 yards, though for clarity the latter unit is properly called "Shooters MOA," or SMOA.
The other common unit is the mil, which simply means thousandth. For example, at 100 yards a mil is 100 yards / 1000 = 3.6". Some more benign confusion also persists around this term, with some assuming "mil" is short for milliradian, which is another angular unit. Fortunately, a milliradian — 3600" tan (1/1000 radians) ≈ 3.600001" inches at 100 yards — is almost exactly equal to a mil so there’s no harm interchanging mil, mrad, milrad, and milliradian.
NB: 1 mil = 3.6 SMOA \(\approx\) 3.44 MOA. See Angular Size for detailed illustrations and conversion formulas.
Examples
One of the important questions addressed here is what to measure in order to determine the intrinsic precision of a shooting system, and what sample size is sufficient to achieve any degree of statistical significance.
Following are common measurements used in the industry:
- Extreme Spread of a 3-shot group, usually at 100 yards. This is statistically almost meaningless, especially when there is no reference to how many 3-shot groups were sampled. (An extended practical, and amusing, critique of the 3-shot group is archived here.)
- Extreme Spread of a 5-shot group, sometimes excluding the worst shot. Hardly any better.
- Average, Max, and Min Extreme Spread of five 5-shot groups. (This is the protocol used by the NRA's magazines and is actually rather efficient.)
- The US Army Marksmanship Unit at Ft. Benning, GA uses a minimum of 3 consecutive 10-shot groups fired with the rifle in a machine rest when testing service rifles. Armed forces also often explicitly uses the more statistically powerful Mean Radius and Circular Error Probable measures.
Measures
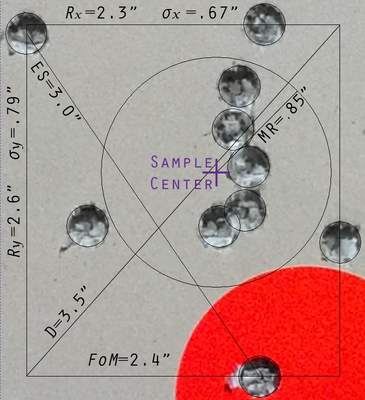
Eight different measures have been used to characterize the dispersion of bullet holes in a sample target. Some are easier to calculate than others.
In the following formulas assume that we are looking at a target reflecting n shots and that we are able to determine the center coordinates x and y for each shot.
As is customary, the mean value of a set of values \(\lbrace x \rbrace\) is called "x-bar" and defined as \(\bar{x} \equiv \sum_{}^n x_i / n\).
(There are some methods for dealing with the case of targets with ragged holes in which we can't determine the precise coordinates of each shot.)
Mean Radius (MR)
- \(\bar{R} = \sum_{}^n r_i / n\) where \(r_i = \sqrt{(x_i - \bar{x})^2 + (y_i - \bar{y})^2}\)
As we will see in Closed Form Precision, the Mean Radius is typically only 6% larger than the Circular Error Probable. Since this is within the margin of error of most real-world usage the terms MR and CEP may be casually interchanged.
Circular Error Probable (CEP)
CEP(p), for \(p \in [0, 1)\), is the radius of the smallest circle that covers proportion p of the shot group. When p is not indicated it is assumed to be 50%, which is the median shot radius.
Horizontal and Vertical Variance
- \(\sigma_h^2 = \frac{\sum^{n}(x_i - \bar{x})^2}{n - 1}, \quad \sigma_v^2 = \frac{\sum^{n}(y_i - \bar{y})^2}{n - 1}\)
(Often these will be given as standard deviations, which is just the square root of variance.)
Radial Standard Deviation (RSD)
RSD is typically defined in the Prior Art as \(\sqrt{\sigma_x^2 + \sigma_y^2}\). This does not express the standard deviation of shot radii. However it turns out to be \(\sqrt{2}\) times the biased estimator of the Closed Form Precision model and has therefore served as a useful reference.
In order to avoid confusion with this measure that is both biased and misnamed we will try to avoid any further reference to RSD.
Note that in general the actual standard deviation of radii \(r_i\) is not easy to calculate: When \(\sigma_x \neq \sigma_y\) the variance of radii is \(\frac{\sigma_x^2}{\pi} (\pi - 2 K^2(1 - \frac{\sigma_y^2}{\sigma_x^2})) + \sigma_y^2\) where K is the complete elliptic integral.
In the special case that \(\sigma_x = \sigma_y\) then, per the Rayleigh model described in Closed Form Precision, we get the following simple formula:
- \(RSD = \sigma \sqrt{\frac{4 - \pi}{2}}\)
Diagonal
Let \(\hat{X} = x_\max - x_\min, \quad \hat{Y} = y_\max - y_\min\) — i.e., the ranges of x and y values.
The diagonal \(D = \sqrt{\hat{X}^2 + \hat{Y}^2}\) is the length of the diagonal line through the smallest rectangle covering the sample group.
Figure of Merit
FoM = \((\hat{X} + \hat{Y}) / 2\) is the average extreme width and height of the group.
Covering Circle Radius
CCR is the radius of the smallest circle containing all shot centers. This will either pass through the two extreme points – in which case CCR = (Extreme Spread) / 2 – or else it will pass through three outside points.
Extreme Spread
The Extreme Spread \(ES = \max \sqrt{(x_i - x_j)^2 - (y_i - y_j)^2)}\) is the largest distance between any two points, i and j, in the group.
Which Measure is Best?
Precision Models will detail the mathematical relationships between many of these measures.
Invariant Measures
- Mean Radius
- Circular Error Probable
- Variance
- Standard Deviation
It is worth noting that these first four measures do not vary with group size. I.e., taking more shots tightens their confidence interval but doesn't change their expected value.
In fact we will see that when \(\sigma_h = \sigma_v\) each of these four measures is just a scalar function of σ, so they all convey the same underlying information.
Range Statistics
- Extreme Spread
- Diagonal
- Figure of Merit
- Covering Circle Radius
These measures increase with group size. They are more commonly used because they are easier to calculate. But they are statistically far weaker because they virtually ignore inner data points.
Next: Precision Models