Difference between revisions of "FAQ"
(→What is sigma (σ) and what does it mean?) |
|||
| Line 4: | Line 4: | ||
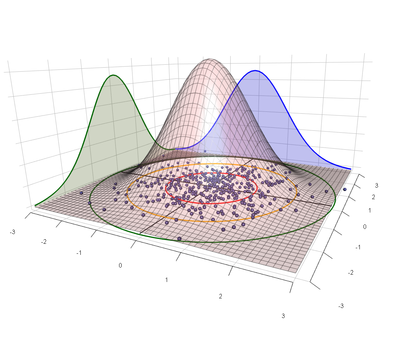
[[File:Bivariate.png|400px|thumb|right|Distribution of samples from a symmetric bivariate normal distribution. Axis units are multiples of σ.]] | [[File:Bivariate.png|400px|thumb|right|Distribution of samples from a symmetric bivariate normal distribution. Axis units are multiples of σ.]] | ||
| − | The [[Closed_Form_Precision#Symmetric_Bivariate_Normal_.3D_Rayleigh_Distribution|most convenient statistical model]] for shooting precision uses a bivariate | + | The [[Closed_Form_Precision#Symmetric_Bivariate_Normal_.3D_Rayleigh_Distribution|most convenient statistical model]] for shooting precision uses a bivariate normal distribution to characterize the point of impact of shots on a target. In this model the same ''σ'' that characterizes the dispersion along each axis is also the parameter for the [http://en.wikipedia.org/wiki/Rayleigh_distribution Rayleigh distribution], which describes how far we expect shots to fall from the center of impact on a target. |
Shooting precision is described using [[Describing_Precision#Units|angular units]], so [[Closed_Form_Precision#Typical_values_of_.CF.83|typical values of ''σ'']] are things like 0.1mil or 0.5MOA. | Shooting precision is described using [[Describing_Precision#Units|angular units]], so [[Closed_Form_Precision#Typical_values_of_.CF.83|typical values of ''σ'']] are things like 0.1mil or 0.5MOA. | ||
| Line 28: | Line 28: | ||
''σ'' also tells us what to expect from other precision measures. For example, [[Range_Statistics#Example_1|on average a five-shot group has an extreme spread of 3''σ'']]. So if ''σ''=0.5SMOA and we are shooting at a 100-yard target we would expect the extreme spread of an average 5-shot group to be 1.5". | ''σ'' also tells us what to expect from other precision measures. For example, [[Range_Statistics#Example_1|on average a five-shot group has an extreme spread of 3''σ'']]. So if ''σ''=0.5SMOA and we are shooting at a 100-yard target we would expect the extreme spread of an average 5-shot group to be 1.5". | ||
| + | |||
| + | == What is the best number of shots per group? == | ||
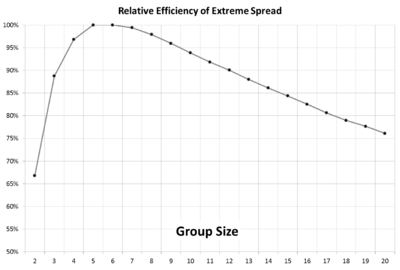
| + | [[File:Extreme Spread Relative Efficiency.png|400px|thumb|right|Relative Efficiency of Extreme Spread estimation by group size.]] | ||
| + | [[Range_Statistics#Efficient_Estimators|Five or six]]. | ||
| + | |||
| + | If you intend to use "group size" (e.g., Extreme Spread) to estimate precision then you'll spend 13% more bullets shooting 3-shot groups to get the same statistical confidence. | ||
| + | |||
| + | Four-shot groups are only 3% less efficient than five-shot groups, so practically just as good. | ||
| + | |||
| + | <br clear=all> | ||
| + | |||
== How many shots do I need to sight in? == | == How many shots do I need to sight in? == | ||
== How do I tell whether ''A'' is more accurate than ''B''? == | == How do I tell whether ''A'' is more accurate than ''B''? == | ||
Revision as of 11:58, 25 May 2014
Contents
What is sigma (σ) and what does it mean?
σ ("sigma") is a single number that characterizes precision. In statistics σ represents standard deviation, which is a measure of dispersion, and which is a parameter for the normal distribution.
The most convenient statistical model for shooting precision uses a bivariate normal distribution to characterize the point of impact of shots on a target. In this model the same σ that characterizes the dispersion along each axis is also the parameter for the Rayleigh distribution, which describes how far we expect shots to fall from the center of impact on a target.
Shooting precision is described using angular units, so typical values of σ are things like 0.1mil or 0.5MOA.
With respect to shooting precision the meaning of σ has an analog to the "68-95-99.7 rule" for standard deviation: The 39-86-99 rule. I.e., we expect 39% of shots to fall within 1σ of center, 86% within 2σ, and 99% within 3σ. Other common values are listed in the following table:
| Name | Multiple of σ | Shots Covered |
|---|---|---|
| 1 | 39% | |
| CEP | 1.18 | 50% |
| MR | 1.25 | 54% |
| 2 | 86% | |
| 3 | 99% |
So, for example, if σ=0.5MOA then 99% of shots should stay within a circle of radius 3σ=1.5MOA.
σ also tells us what to expect from other precision measures. For example, on average a five-shot group has an extreme spread of 3σ. So if σ=0.5SMOA and we are shooting at a 100-yard target we would expect the extreme spread of an average 5-shot group to be 1.5".
What is the best number of shots per group?
If you intend to use "group size" (e.g., Extreme Spread) to estimate precision then you'll spend 13% more bullets shooting 3-shot groups to get the same statistical confidence.
Four-shot groups are only 3% less efficient than five-shot groups, so practically just as good.