FAQ
What is sigma (σ) and what does it mean?
σ ("sigma") is a single number that characterizes precision. In statistics σ represents standard deviation, which is a measure of dispersion, and which is a parameter for the normal distribution.
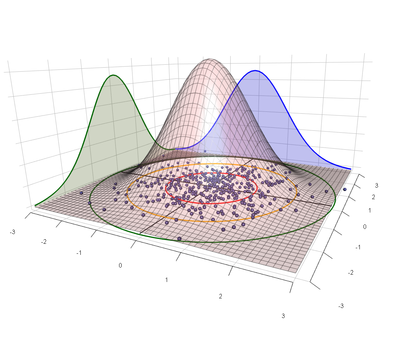
The most convenient statistical model for shooting precision uses a bivariate normal distribution to characterize the point of impact of shots on a target. In this model the same σ that characterizes the dispersion along each axis is also the parameter for the Rayleigh distribution, which describes how far we expect shots to fall from the center of impact on a target.
Shooting precision is described using angular units, so typical values of σ are things like 0.1mil or 0.5MOA.
With respect to shooting precision the meaning of σ has an analog to the "68-95-99.7 rule" for standard deviation: The 39-86-99 rule. I.e., we expect 39% of shots to fall within 1σ of center, 86% within 2σ, and 99% within 3σ. Other common values are listed in the following table:
| Name | Multiple of σ | Shots Covered |
|---|---|---|
| 1 | 39% | |
| CEP | 1.18 | 50% |
| MR | 1.25 | 54% |
| 2 | 86% | |
| 3 | 99% |
So, for example, if σ=0.5MOA then 99% of shots should stay within a circle of radius 1.5MOA.