Precision Models

Previous: Describing Precision

Models of Dispersion

We have four options for measuring and analyzing precision:

1. Closed Form Precision
2. Circular Error Probable
3. Elliptic Error Probable
4. Range Statistics

Before selecting one consider the following background:

General Bivariate Normal

The normal, a.k.a. Gaussian, distribution is the broadly accepted model of a random variable like the dispersion of a physical gunshot from its center point. The normal distribution is parameterized by its mean and standard deviation, or \((\mu, \sigma)\). As explained in What is Precision? we are only interested in the dispersion component, since the center point of impact is controlled by sighting in the gun (i.e., adjusting its aiming device). Therefore we will assume that a gunner can dial \(\mu = 0\), and leave that parameter out of the question in what follows.

Since we are interested in shot dispersion on a two-dimensional target we will look at a bivariate normal distribution, which has separate parameters for the standard deviation in each dimension, \(\sigma_x, \sigma_y\), as well as a correlation parameter ρ.

Uncorrelated Bivariate Normal

We don't have any compelling evidence that in general there is, or should be, correlation between the horizontal and vertical dispersion of gunshots. Therefore, for most of our analysis we will assume ρ = 0.

We do know that targets can often exhibit vertical or horizontal stringing, and therefore \(\sigma_x \neq \sigma_y\). To the extent these parameters are not equal they produce elliptical instead of circular shot groups.

However, we know some of the significant sources of stringing and can potentially factor them out:

1. The primary source of x-specific variance is crosswind. If we measure the wind while shooting we can bound and remove a “wind variance” term from that axis. E.g., "Suppose the orthogonal component of wind is ranging at random from 0-10mph during the shooting. Given lag-time t this will expand the no-wind horizontal dispersion at the target by \(\sigma_w\)." Since variances are additive we could adjust \(\sigma_x\) via the equation \({\sigma'}_x^2 = \sigma_x^2 - \sigma_w^2\).
2. The primary source of y-specific variance is muzzle velocity, which we can actually measure with a chronograph (or assert) and then remove from that axis. E.g., "If standard deviation of muzzle velocity is \(\sigma_{mv}\) then, given the bullet's ballistic model for the given target distance, the vertical spread attributable to that is some \(\sigma_v\). Here too we can remove this known source of dispersion from our samples via the equation \({\sigma'}_y^2 = \sigma_y^2 - \sigma_v^2\). This adjustment is shown in several of the examples:
   • 22LR CCI 40gr HV 40-shot 100-yard Example
   • 300BLK Subsonic 20-shot 100-yard Example

Statistical Analysis of Dispersion

In view of the preceding:

1. The Closed Form Precision model requires that we assume the shot group is, or can be normalized to be, a fairly symmetric bivariate Gaussian process, but allows for the most convenient estimators and analysis. Therefore, whenever \(\sigma_x \approx \sigma_y\) we prefer this approach.
2. Circular Error Probable disregards any ellipticity in the actual shot process in order to characterize precision using a single parameter. Since most of precision estimation is for the purposes of comparing loads, rifles, and shooters, we need a single number and we don't care if the dispersion is elliptic: tighter is always better.
3. Elliptic Error Probable allows for a full characterization of the General Bivariate Normal model. For some applications – e.g., computing hit probabilities on non-circular targets – we want to preserve statistically significant ellipticity. And for a few – e.g., harmonic dampening, and perhaps shooter technique correction – the orientation of the ellipse produced by non-zero ρ could be helpful if it can be estimated.
4. Extreme Spread and the other Range Statistics, which increase with group size n, do not have any useful functional forms. The characteristics of these measures have to be derived from Monte Carlo simulation. Therefore we rely only on the central limit theorem to estimate and evaluate those. They are the least efficient statistics and are preserved only because they are so easy to measure in the field and so familiar to shooters.

Examples

See Measuring Tools for convenient ways of measuring and analyzing precision.

The 3-shot Group

Sample 3-shot group with 1/2" extreme spread. Sample center is in red. Each shot has r = .29".

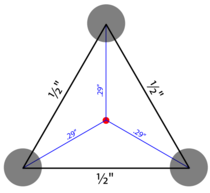
A rifle builder sends you a 3-shot group measuring ½" between each of three centers to prove how accurate your rifle is. What does that really say about the gun's accuracy? In the best case – i.e.:

1. The group was actually fired from your gun
2. The group was actually fired at the distance indicated (in this case 100 yards)
3. The group was not cherry-picked from a larger sample – e.g., the best of an unknown number of test 3-shot groups
4. The group was not clipped from a larger group (in the style of the "Texas Sharpshooter")

— if all of these conditions are satisfied, then we have a statistically valid sample. In this case our group is an equilateral triangle with ½" sides. A little geometry shows the distance from each point to sample center is \(r_i = \frac{1}{2 \sqrt{3}} \approx .29"\).

The Rayleigh estimator \(\widehat{\sigma_R^2} = c_B(3) \frac{\sum r_i^2}{6} = \frac{3}{2} \frac{1}{24} = \frac{1}{16}\). So \(\hat{\sigma} = c_G(2n - 1) \sqrt{1/16} = (\frac{4}{3}\sqrt{\frac{2}{\pi}})\frac{1}{4} \approx .25MOA\). Not bad! But not very significant. Let's check the confidence intervals: For α = 5% (i.e., 95% confidence intervals)

  \(\chi_1^2(4) \approx 0.484, \quad \chi_2^2(4) \approx 11.14\). Therefore,

  \(0.02 \approx \frac{1}{4 \chi_2^2} \leq \widehat{\sigma_R^2} \leq \frac{1}{4 \chi_1^2} \approx 0.52\), and

  \(0.16 \leq \hat{\sigma} \leq 0.76\)

so with 95% certainty we can only say that the gun's true precision σ is somewhere in the range from approximately 0.2MOA to 0.8MOA.