Precision Models
Statistical Models of Dispersion
The General Bivariate Normal
The normal, a.k.a. Gaussian, distribution is the accepted model of a random variable like the dispersion of a physical gunshot from its center point. The normal distribution is parameterized by its mean and standard deviation, or \((\mu, \sigma)\). As explained in What is Precision? we are only interested in the dispersion component, since the center point of impact is controlled by sighting in the gun (i.e., adjusting its aiming device). Therefore we will assume that a gunner can dial \(\mu = 0\), and leave that parameter out of the question in what follows.
Since we are interested in shot dispersion on a two-dimensional target we will look at a bivariate normal distribution, which has separate parameters for the standard deviation in each dimension, \(\sigma_x, \sigma_y\), as well as a correlation parameter ρ.
We don't have any compelling evidence that in general there is, or should be, correlation between the horizontal and vertical dispersion of gunshots. Therefore, for purposes of modelling we set ρ = 0.
We do know that targets can often exhibit vertical or horizontal stringing, and therefore \(\sigma_x \neq \sigma_y\). To the extent these parameters are not equal they produce elliptical instead of round shot groups.
However, we know some of the significant sources of stringing and can factor them out:
- The primary source of x-specific variance is crosswind. If we measure the wind while shooting we can bound and remove a “wind variance” term from that axis. E.g., "Suppose the orthogonal component of wind is ranging at random from 0-10mph during the shooting. Given time-of-flight t this will expand the no-wind horizontal dispersion at the target by \(\sigma_w\)." Closed-form equation for this?
- The primary source of y-specific variance is muzzle velocity, which we can actually measure with a chronograph (or assert) and then remove from that axis. E.g., "If standard deviation of muzzle velocity is \(\sigma_{mv}\) then, given time-of-flight t the vertical spread attributable to that is some \(D(t, \sigma_{mv}\))." Closed-form equation for this?
Substantially asymmetric shot groups will be addressed in a separate section.
Symmetric Bivariate Normal = Rayleigh
After factoring out the known sources of asymmetry in the bivariate normal model we believe that shot groups are sufficiently symmetric that we can assume \(\sigma_x = \sigma_y\). In this case the dispersion of shots is modeled by a symmetric bivariate normal, which is equivalent[1] to the Rayleigh distribution, described by a single parameter σ.
NB: It is common to describe normal distributions using variance, or \(\sigma^2\), because variances have some convenient linear characteristics that are lost when we take the square root. For similar reasons many prefer to describe the Rayleigh distribution using a parameter \(\gamma = \sigma^2\). To clarify our parameterization the σ we will be describing is the standard deviation of the bivariate normal distribution, and the parameter that produces the following pdf for the Rayleigh distribution:
- \(\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}\)
Estimating σ
The Rayleigh distribution will be most convenient for Predicting Precision, but when estimating σ from sample sets we will most often use methods associated with the normal distribution for one essential reason: We never observe the true center of the distribution. When we calculate the center of a group on a target it will almost certainly be some distance from the true center, and thus underestimate the true distance of the sample shots to the distribution center. (Average distance from sample center to true center is listed in the second column of Media:Sigma1ShotStatistics.ods.) The Rayleigh describes the distribution of shots from the (unobservable) true center. When the center is unknown we have to use the sample center, and we fall back on characteristics of the normal distribution with unknown mean.
Correction Factors
The following three correction factors will be used throughout this statistical inference and deduction.
Note that all of these correction factors are > 1, are significant for very small n, and converge towards 1 as \(n \to \infty\). Their values are listed for n up to 100 in Media:Sigma1ShotStatistics.ods. File:SymmetricBivariate.c uses Monte Carlo simulation to confirm that their application produces valid corrected estimates.
Bessel correction factor
The Bessel correction removes bias in sample variance.
- \(c_{B}(n) = \frac{n}{n-1}\)
Gaussian correction factor
The Gaussian correction (sometimes called \(c_4\)) removes bias introduced by taking the square root of variance.
- \(\frac{1}{c_{G}(n)} = \sqrt{\frac{2}{n-1}}\,\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)} \, = \, 1 - \frac{1}{4n} - \frac{7}{32n^2} - \frac{19}{128n^3} + O(n^{-4})\)
The third-order approximation is adequate. The following spreadsheet formula gives a more direct calculation: =EXP(LN(SQRT(2/(N-1))) + GAMMALN(N/2) - GAMMALN((N-1)/2))
Rayleigh correction factor
The unbiased estimator for the Rayleigh distribution is also for \(\sigma^2\). The following corrects for the concavity introduced by taking the square root to get σ.
- \(c_{R}(n) = 4^n \sqrt{\frac{n}{\pi}} \frac{ N!(N-1)!} {(2N)!}\) [2]
To avoid overflows this is better calculated using log-gammas, as in the following spreadsheet formula: =EXP(LN(SQRT(N/PI())) + N*LN(4) + GAMMALN(N+1) + GAMMALN(N) - GAMMALN(2N+1))
Data
In the following formulas assume that we are looking at a target reflecting n shots and that we are able to determine the center coordinates x and y for each shot.
(One easy way to compile these data is to process an image of the target through a program like OnTarget Precision Calculator.)
Variance Estimates
For a single axis the unbiased estimate of variance for a normal distribution is \(s_x^2 = \frac{\sum (x_i - \bar{x})^2}{n-1} \), from which the unbiased estimate of standard deviation is \(\widehat{\sigma_x} = c_G(n) \sqrt{(s_x^2)}\).
Since we are assuming that the shot dispersion is jointly independent and identically distributed along the x and y axes we improve our estimate by aggregating the data from both dimensions. I.e., we look at the average sample variance \(s^2 = (s_x^2 + s_y^2)/2\), and \(\hat{\sigma} = c_G(2n-1) \sqrt{s^2}\). This turns out to be identical to the Rayleigh estimator.
Rayleigh Estimates
The Rayleigh distribution describes the random variable R defined as the distance of each shot from the center of the distribution. Again, we never get to observe the true center, so we begin by calculating the sample center \((\bar{x}, \bar{y})\). Then for each shot we can compute the sample radius \(r_i = \sqrt{(x_i - \bar{x})^2 + (y_i - \bar{y})^2}\).
The unbiased Rayleigh estimator is \(\widehat{\sigma_R^2} = c_B(n) \frac{\sum r_i^2}{2n} = \frac{c_B(n)}{2} \overline{r^2}\), which is literally a restatement of the combined variance estimate \(s^2\). Hence the unbiased parameter estimate is once again \(\hat{\sigma} = c_G(2n-1) \sqrt{\widehat{\sigma^2}}\)
Confidence Intervals
Siddiqui[3] shows that the confidence intervals are given by the \(\chi^2\) distribution with 2n degrees of freedom. However this assumes we know the true center of the distribution. We lose two degrees of freedom (one in each dimension) by using the sample center, so we actually have only 2(n - 1) degrees of freedom. To find the (1 - α) confidence interval, first find \(\chi_1^2, \ \chi_2^2\) where:
- \(Pr(\chi^2(2(n-1)) \leq \chi_1^2) = \alpha/2, \quad Pr(\chi^2(2(n-1)) \leq \chi_2^2) = 1 - \alpha/2\)
For example, using spreadsheet functions we have \(\chi_1^2\) = CHIINV(α/2, 2n-2),\(\quad \chi_2^2\) = CHIINV((1-α/2), 2n-2).
Now the confidence intervals are given by the following:
- \(\widehat{\sigma^2} \in \left[ \frac{2(n-1)\overline{r^2}}{\chi_2^2}, \ \frac{2(n-1)\overline{r^2}}{\chi_1^2} \right]\)
- \(\widehat{\sigma} \in \left[ c_G(2n-1) \sqrt{\frac{2(n-1)\overline{r^2}}{\chi_2^2}}, \ c_G(2n-1) \sqrt{\frac{2(n-1)\overline{r^2}}{\chi_1^2}} \right]\)
Examples
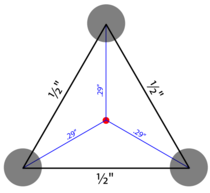
The 3-shot Group
A rifle builder sends you a 3-shot group measuring ½" between each of three centers to prove how accurate your rifle is. What does that really say about the gun's accuracy? In the best case – i.e.:
- The group was actually fired from your gun
- The group was actually fired at the distance indicated (in this case 100 yards)
- The group was not cherry-picked from a larger sample – e.g., the best of an unknown number of test 3-shot groups
- The group was not clipped from a larger group (in the style of the "Texas Sharpshooter")
— if all of these conditions are satisfied, then we have a statistically valid sample. In this case our group is an equilateral triangle with ½" sides. A little geometry shows the distance from each point to sample center is \(r_i = \frac{1}{2 \sqrt{3}} \approx .29"\).
The Rayleigh estimator \(\widehat{\sigma^2} = c_B(3) \frac{\sum r_i^2}{6} = \frac{3}{2} \frac{1}{24} = \frac{1}{16}\). So \(\hat{\sigma} = c_G(2n - 1) \sqrt{1/16} = (\frac{4}{3}\sqrt{\frac{2}{\pi}})\frac{1}{4} \approx .25MOA\). Not bad! But not very significant. Let's check the confidence intervals: For α = 5% (i.e., 95% confidence intervals)
- \(\chi_1^2(4) \approx 0.484, \quad \chi_2^2(4) \approx 11.14\). Therefore,
- \(0.03 \approx \frac{1}{3 \chi_2^2} \leq \widehat{\sigma^2} \leq \frac{1}{3 \chi_1^2} \approx 0.69\), and
- \(0.18 \leq \hat{\sigma} \leq 0.88\)
so with 95% certainty we can only say that the gun's true precision σ is somewhere in the range from approximately 0.2MOA to 0.9MOA.
Inference from Extreme Spreads
What can we deduce about the precision of a gun from extreme spread samples?
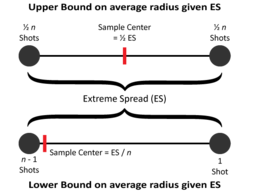
Without knowing the radius of each shot we can still put upper and lower bounds on the group's radii. The image at right shows that if we only know the Extreme Spread ES and the number of shots n in the group then we can assert the following bounds on the average radius:
- \(\overline{r_U} = ES / 2\) is an upper bound, with \(\overline{r_U^2} = (ES / 2)^2\)
- \(\overline{r_L} = \frac{1}{n} ((n - 1) \frac{ES}{n} + ES(1 - \frac{1}{n})) = \frac{2(n - 1)}{n^2} ES\) is a lower bound, with \(\overline{r_L^2} = (n - 1) (\frac{ES}{n})^2\)
We can then derive confidence intervals using these bounded radii:
- \(\frac{2(n-1)\overline{r_L^2}}{\chi_2^2} \leq \widehat{\sigma^2} \leq \frac{2(n-1)\overline{r_U^2}}{\chi_1^2}\)
Example
The standard precision measure given in the NRA's magazines is the minimum, maximum, and average extreme spread of five 5-shot groups. Suppose they show an average group size of 1MOA: What is the implied precision parameter, and what is our confidence in it?
Note that both the σ estimator and confidence intervals depend on the sample values of each shot, \(r_i^2\). We can't observe the r values directly, but we can put bounds on them. In this case we have five groups of five shots, and we can bound each group based on its stated extreme spread. To simplify the example let's just assume that each group had the same extreme spread of 1MOA. So we have n = 25 shots with the same upper and lower bounds, and ES = 1. From the formulas for the bounds and for the Rayleigh estimator:
- \(\widehat{\sigma_U^2} = \frac{c_B(25)}{2} (\frac{1}{4}) = \frac{25}{192} \approx .13\)
- \(\widehat{\sigma_L^2} = \frac{c_B(25)}{2} (\frac{24}{625}) = \frac{25}{48} (\frac{24}{625}) = \frac{1}{50} = .02\)
Taking square roots and applying the correction \(c_G(49) \approx 1.00522\) we have:
- \(\widehat{\sigma_L} \approx 0.14 \leq \widehat{\sigma} \leq 0.36 \approx \widehat{\sigma_U}\)
Our 95% confidence intervals are based on:
- \(\chi_1^2(48) \approx 30.75, \quad \chi_2^2(48) \approx 69.02\). Therefore, using the lower bound \(\overline{r_L^2}\) for the lower confidence interval, and the upper bound \(\overline{r_U^2}\) for the upper confidence interval, we have:
- \(0.060 \leq \widehat{\sigma^2} \leq 0.17\), and \(0.24 \leq \hat{\sigma} \leq 0.42\).
As we see in Predicting_Precision#Spread_Measures the expected extreme spread from 5-shot groups is 3.06 σ. So based on the NRA data we can at least say that with 95% certainty the average of future 5-shot group extreme spreads should be in the range (.75, 1.28)MOA