Difference between revisions of "Projectile Dispersion Classifications"

From ShotStat
Jump to: navigation, search
(Created page with "Before considering the mathematical models that will be used for the actual statistical analysis, let's consider the assumptions of various dispersion models and hence the int...")
 
(→‎Simplification of the Hoyt distribution into Special Cases)
 
(66 intermediate revisions by 3 users not shown)
Line 1: Line 1:
−
Before considering the mathematical models that will be used for the actual statistical analysis, let's consider the assumptions of various dispersion models and hence the intrinsic functions of how shots are dispersed. The [http://en.wikipedia.org/wiki/Normal_distribution Normal distribution] is the broadly assumed probability model used for a single random variable and it is characterized by its mean <math>(\bar{x})</math> and standard deviation <math>(\sigma)</math>. Since we are interested in shot dispersion on a two-dimensional target we will assume that the two dimensional analog of the Normal distribution, the [http://en.wikipedia.org/wiki/Bivariate_normal_distribution Bivariate Normal Distribution]. This distribution describes, at least approximately, the dispersion of a gunshots about their center point, (<math>\bar{h}</math> and <math>\bar{v}</math>). The bivariate normal distribution  also has separate parameters for the standard deviation in each dimension, <math>\sigma_h</math> and <math>\sigma_v</math>, as well as a correlation parameter ''ρ''. The full bivariate normal distribution is thus:<br >
+
{|align=right
 +
  |__TOC__
 +
  |}
 +
Before considering the measurements that will be used for the actual statistical analysis, let's consider the assumptions about projectile dispersion about the Center of Impact (COI) and how sets of those assumptions might be grouped into different classifications. The various classifications will offer insight as to the fundamental patterns expected for shots and insights to the interactions of various measures. Thus an understanding of the basic assumptions about projectile dispersion is key in being able to effectively use the measures.
 +
 
 +
The COI is the only true point of reference which can be calculated from the pattern of shots on a target. Thus the COI is the reference point for precision measurements. The overall error that we are interested in measuring is the sum of all the various interactions that make multiple projectiles shot to the same point of aim (POA) disperse about the COI. 
 +
 
 +
Since we are primarily interested in the dispersion relative to the COI, the overall assumption is that the weapon could be properly sighted so that the COI would be the same as the POA. In practice this is achieved by [[FAQ#How_many_shots_do_I_need_to_sight_in.3F| adjusting the weapon's sights]]. Thus in order to isolate projectile dispersion, all of the factors of internal and external ballistics that cause a bias to the COI on a target will be ignored. For example, for the purposes of classifying projectile dispersion, accuracy errors due to POA errors will be ignored. 
 +
 
 +
The [http://en.wikipedia.org/wiki/Normal_distribution Normal distribution] is the broadly assumed probability model used for a single random variable and it is characterized by its mean <math>(\bar{x})</math> and standard deviation <math>(\sigma)</math>. The [http://en.wikipedia.org/wiki/Central_limit_theorem central limit theorem] shows that for measures for the "average" shot, or averages of multiple targets are used, then for "large" samples the averages will conform to Normal distribution even if the fundamental distribution is not a normal distribution.
 +
 
 +
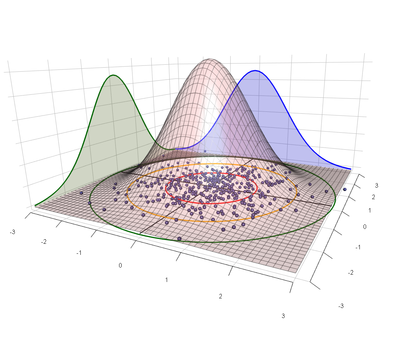
[[File:Bivariate.png|400px|thumb|right|Distribution of samples from a symmetric bivariate normal distribution.  Axis units are multiples of σ.]]
 +
 
 +
Since we are interested in shot dispersion on a two-dimensional target we will assume that the horizontal and vertical dispersions of the population of shots are each Normal distributions. Thus the horizontal dispersion will have mean <math>\mu_H</math> and standard deviation <math>\sigma_H</math>. The vertical dispersion will have mean <math>\mu_V</math> and standard deviation <math>\sigma_V</math>. Then a further assumption is made by assuming that the two dimensional expansion of the Normal distribution the [http://en.wikipedia.org/wiki/Multivariate_normal_distribution#Non-degenerate_case Bivariate Normal distribution], applies. This adds an additional term the  [http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient correlation parameter ''ρ'']. (See also: [[What is ρ in the Bivariate Normal distribution?]]) Thus the expectation is that distribution should then describe, the dispersion of a gunshots about the COI, (<math>\mu_H</math> and <math>\mu_V</math>). The full bivariate normal distribution is thus:<br >
 
&nbsp;&nbsp;&nbsp;&nbsp;<math>
 
&nbsp;&nbsp;&nbsp;&nbsp;<math>
−
     f(h,v) =
+
     f(H,V; \mu_H, \mu_V, \sigma_H, \sigma_V, \rho) =
−
       \frac{1}{2 \pi  \sigma_h \sigma_v \sqrt{1-\rho^2}}
+
       \frac{1}{2 \pi  \sigma_H \sigma_V \sqrt{1-\rho^2}}
 
       \exp\left(
 
       \exp\left(
 
         -\frac{1}{2(1-\rho^2)}\left[
 
         -\frac{1}{2(1-\rho^2)}\left[
−
           \frac{(h-\bar{h})^2}{\sigma_h^2} +
+
           \frac{(H-\mu_H)^2}{\sigma_H^2} +
−
           \frac{(v-\bar{v})^2}{\sigma_v^2} -
+
           \frac{(V-\mu_V)^2}{\sigma_V^2} -
−
           \frac{2\rho(h-\bar{h})(v-\bar{v})}{\sigma_h \sigma_v}
+
           \frac{2\rho(H-\mu_H)(V-\mu_V)}{\sigma_H \sigma_V}
 
         \right]
 
         \right]
 
       \right)
 
       \right)
 
   </math>
 
   </math>
  
−
For the overall equation note that the following restrictions apply:<br />
+
where:<br />
 
&nbsp;&nbsp;&nbsp;&nbsp;<math>-1 &le; \rho &le; 1</math><br />
 
&nbsp;&nbsp;&nbsp;&nbsp;<math>-1 &le; \rho &le; 1</math><br />
−
&nbsp;&nbsp;&nbsp;&nbsp;<math> \sigma_h>0 </math> and <math> \sigma_v>0 </math>
+
&nbsp;&nbsp;&nbsp;&nbsp;<math> \sigma_H>0 </math> and <math> \sigma_V>0 </math>
 +
 
 +
Note that the above restrictions are not additional restrictions on the model, but rather simply pointing out how the mathematics works. Thus they are more analogous to the mathematical notion that a person can't have a negative age.
 +
 
 +
:{| class="wikitable"
 +
| [[File:Bullseye.jpg|50px]] An ancillary point worth mentioning is that the assuming the Normal distribution in three dimensions leads to the [http://en.wikipedia.org/wiki/Maxwell%E2%80%93Boltzmann_distribution Maxwell–Boltzmann distribution] which is the foundation of the ideal gas laws.
 +
|}
 +
 
 +
= Simplification of the Hoyt distribution into Special Cases =
  
−
Since we are primarily interested in the dispersion component, the overall assumption is that weapon is properly sighted so that the center of impact is the same as the point of aim. In practice this can be achieved with a simple translation of the horizontal and vertical coordinates from absolute values to values relative to the average point of impact. Therefore the terms controlled by [[FAQ#How_many_shots_do_I_need_to_sight_in.3F|sighting in the gun]] (<math>\bar{h}</math> and <math>\bar{v}</math>) drop out in the simplification of the dispersion equation.  
+
To eliminate the COI (<math>\mu_H</math>, <math>\mu_V</math>) which makes the equations "messier", a translation of the coordinate system to the COI is desired. Thus:<br />
  
−
== Simplifications into cases ==
+
&nbsp;&nbsp;&nbsp;&nbsp;<math>\mu_h = 0</math>&nbsp;&nbsp;&nbsp;and &nbsp;&nbsp;&nbsp;<math>\mu_v = 0</math><br />
  
−
Looking at the overall equation two different mutually exclusive simplifications can be made:
+
&nbsp;&nbsp;&nbsp;&nbsp;<math>h = H - \mu_H</math>&nbsp;&nbsp;&nbsp;and &nbsp;&nbsp;&nbsp;<math>v = V - \mu_V</math><br />
  
−
* '''Either''' <math>\sigma_h = \sigma_v</math> (equal variances) '''or''' <math>\sigma_h \neq \sigma_v</math> (unequal variances).
+
&nbsp;&nbsp;&nbsp;&nbsp;and&nbsp;&nbsp;<math>\sigma_h = \sigma_H </math>&nbsp;&nbsp; and &nbsp;&nbsp;<math>\sigma_v = \sigma_V </math><br />
−
: Obviously if we could measure both <math>\sigma_h</math> and <math>\sigma_v</math> with a very high precision (e.g 6 significant figures), then the two quantities would never really be equal. But in many cases the assumption is reasonable. In reality since shooters typically collect only a small amount of data, statistical tests will fail to detect a difference unless the difference is great. In such cases the shot pattern would be noticeably elliptical not round.  
+
 
 +
This is a very pragmatic and justifiable consideration since the COI can be measured on the target, and the dispersion about the COI is the aspect of interest when measuring precision. As noted before, by adjusting the weapon's sights the POA can be made to coincide with the COI. Thus this simplification of the dispersion equations is strictly for ease of understanding as is not a limitation on the nature of the dispersion classifications. With the translation of the coordinate system to the COI, then the general bivariate normal equation becomes the Hoyt distribution:<br />
 +
&nbsp;&nbsp;&nbsp;&nbsp;<math>
 +
    f(h,v; \sigma_h, \sigma_v, \rho) =
 +
      \frac{1}{2 \pi  \sigma_h \sigma_v \sqrt{1-\rho^2}}
 +
      \exp\left(
 +
        -\frac{1}{2(1-\rho^2)}\left[
 +
          \frac{h^2}{\sigma_h^2} +
 +
          \frac{v^2}{\sigma_v^2} -
 +
          \frac{2\rho hv}{\sigma_h \sigma_v}
 +
        \right]
 +
      \right)
 +
  </math>
 +
 
 +
Looking at this equation two other different mutually exclusive simplifications can be readily seen:
 +
 
 +
* '''Either''' <math>\sigma_h = \sigma_v</math> (equal standard deviations) '''or''' <math>\sigma_h \neq \sigma_v</math> (unequal standard deviations).
 +
: Obviously if we could measure both <math>\sigma_h</math> and <math>\sigma_v</math> with a very high precision (e.g 6 significant figures), then the two quantities would never really be equal. But in many cases the assumption is reasonable. In reality since shooters typically collect only a small amount of data, statistical tests will fail to detect a difference unless the difference is great. In such cases the shot pattern would be noticeably elliptical, not round.  
  
 
* '''Either''' <math>\rho = 0</math> (uncorrelated) '''or''' <math>\rho \neq 0</math> (correlated).  
 
* '''Either''' <math>\rho = 0</math> (uncorrelated) '''or''' <math>\rho \neq 0</math> (correlated).  
  
−
The pair of mutually exclusive assumptions thus results in four cases for analytical evaluation.  
+
:{| class="wikitable"
 +
| [[File:Bullseye.jpg|50px]]: !! CAREFUL !! '''[http://en.wikipedia.org/wiki/Correlation_does_not_imply_causation Correlation does not imply causation]'''
 +
 
 +
: There is somewhat famous example. A researcher gathered statistics for stork sightings and births in a particular county over a twenty year period. Analysis of the data showed that over the twenty year period both stork sightings and births had increased with a very significant linear correlation. From the data you might erroneously infer that storks do bring babies! 
 +
|}
  
−
== Error Propagation ==
+
The pair of mutually exclusive assumptions thus results in four cases for analytical evaluation as shown in the Table below. There is one case that results in circular groups, and three that result in elliptical groups. As the different in variances gets greater, or the further <math>\rho</math> is from 0, then the ellipse will be more pronounced.
  
−
In general shooting has a number of different error sources. The "basic" assumption is that the error sources are normally distributed and independent. Thus for example the vertical error component would be something like:<br>
+
{| class="wikitable"  
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\sigma_v^2 = \sigma_{v,Weapon}^2 + \sigma_{v,Ammunition}^2 + \sigma_{v,shooter}^2</math><br />
+
|+ Group Shape vs. Assumptions (COI at Origin)
−
and there would similar equations for <math>\sigma_h^2</math> and <math>\sigma_{RSD}^2</math>.
+
|-
 +
|
 +
| <math>\sigma_h \approx \sigma_v</math>
 +
| <math>\sigma_h \neq \sigma_v</math>
 +
|-
 +
| <math>\rho \approx 0</math>
 +
| Case 1 - Circular Groups
 +
* special case is the Rayleigh Distribution
 +
* Parameter(s) to fit (other than COI):
 +
: - <math>\sigma_{\Re}</math> (pooled value of <math>\sigma_h</math> and <math>\sigma_v</math>)
 +
| Case 3 - Elliptical Groups
 +
* special case is the Orthogonal Elliptical Distribution
 +
* Major axis of ellipse along<br /> horizontal or vertical axis
 +
* Parameter(s) to fit (other than COI):
 +
: - <math>\sigma_h</math>
 +
: - <math>\sigma_v</math>
 +
|-
 +
| <math>\rho \neq 0</math>
 +
* Major axis of ellipse at an angle to<br />both the horizontal and vertical axes
 +
| Case 2- Elliptical Groups
 +
* Parameter(s) to fit (other than COI):
 +
: - <math>\sigma_{\Re}</math> (pooled value of <math>\sigma_h</math> and <math>\sigma_v</math>)
 +
: - <math>\rho</math>
 +
| Case 4 - Elliptical Groups
 +
* general case of the Hoyt distribution required
 +
* Parameter(s) to fit (other than COI):
 +
: - <math>\sigma_h</math>
 +
: - <math>\sigma_v</math>
 +
: - <math>\rho</math>
 +
|}
  
−
Notes:
+
== Experimental reality of Comparing <math>s_h</math> and <math>s_v</math>==
−
# The error sources can't be measured independently. Only the total error is observable. This is a very important consideration since the total error thus limits the precision which any of the individual error factors can be determined.
 
−
# If any one of the error sources is more than about three times the sum of the other two, then that error source essentially controls the overall error of the measurement.
 
−
# These error sources could be decomposed further into "finer" errors. For instance consider the multitude of variables that a handloader controls when loading a cartridge.
 
−
# The fact that a very small amount of data is typically collected by a shooter greatly limits the overall precision of the mathematical analysis. In statistics this is known as the "small sample" problem. For example to get "good" estimates for the normal distribution parameters <math>\bar{x}</math> and <math>\sigma</math>, 30 measurements are desired.
 
−
# In general for a given sample size of ''n'' measurements the mean, <math>\bar{x}</math>, is determined relatively (i.e as a percentage) much more precisely than the standard deviation, <math>\sigma</math> (or other dispersion factor).
 
  
−
== Stringing ==
+
The table above uses ''approximately equal to'' <math>(\approx)</math> rather than ''strictly  equal to'' <math>( = )</math>. This is an acknowledgement that we are dividing the cases into ones that are close enough to be useful, even though they most certainly are not exact. To be overly persnickety there are two considerations.
  
−
To the extent that either <math>\sigma_h \neq \sigma_v</math> or <math>\rho \neq 0</math> then elliptical shot groups will result instead of circular shot groups. If the shot groups are not round then we have three options. We can:
+
First we can only get experimental estimates from calculations based on sample data for the factors <math>\sigma_h</math>, <math>\sigma_v</math>, <math>\rho</math> and these estimates are at best only good to a scant few significant figures. Thus even though the difference between ''approximately equal to'' and ''strictly equal to'' is under some experimental control there are practical limits. In other words, we can theoretically make the measurements as precise as we want by collecting more data, but it is quickly impractical to do so. (Assume that to double the precision that we have to quadruple the sample size. This exponential increase quickly becomes unmanageable. It is easy to pontificate about averaging over a million targets, but no one is going to shoot that many.) Thus even if <math>\sigma_h \equiv \sigma_v</math> we'd never expect that we'd experimentally get <math>s_h = s_v</math> due to experimental error.  
−
# Isolate the error source experimentally and remove it (for instance weigh gunpowder carefully to remove vertical stringing).  
 
−
# Use a mathematical model for analysis that allows for stringing.
 
−
# Scale the raw data to remove the stringing.  
 
  
−
Obviously the experimental reason for stinging may not be obvious and easy to remove. Experimental designs to isolate and quantify the source of the stringing are beyond this basic discussion at this point, but possible.  
+
Second there is the good enough. Shooting by definition is going to have fairly small sample sizes. So if <math>0.66s_h < s_v < 1.5 s_h</math> then, as a rule of thumb, that is probably good enough. Of course for large sample we would want to tighten the window. The harsh reality is that if <math>s_h</math> and <math>s_v</math> could be measured with great precision (e.g. to ten significant figures), then two values would always be statistically significantly different.  
  
−
There isn't any theoretical ballistic requirement that requires correlation between the horizontal and vertical dispersion of gunshots.  Therefore, most statistical measures implicitly assume <math>\rho = 0</math>. In general if <math>\rho \neq 0</math>, then there would be an elliptical shaped group with the major axis oriented at some angle to the horizontal or vertical axis.  
+
Thus the approximation that <math>\sigma_h \approx \sigma_v</math> will be used unless the variances are known to be statistically significantly different. On the experimental data it is possible to test for a statistically significant difference by using a ratio of <math>s_h^2</math> and <math>s_v^2</math> via the F-Test. The "catch" in using the F test is that the variance has poor precision for small samples. Thus the difference must be great for the F-Test to detect that the two variances are not equal.
  
−
We do know that targets can often exhibit vertical or horizontal stringing as evidenced by an elliptical shaped group along the vertical or horizontal axis respectively. Obviously in such cases <math>\sigma_h \neq \sigma_v</math>.
+
== Simplifications Reduce Number of Coefficients to Fit ==
  
−
:(1) The primary source of horizontal stringing is crosswind. 
+
The Hoyt distribution is general enough to be able to fit all four of the special cases in the table above. The point in making special cases of the Hoyt distribution is to reduce the number of coefficients to fit to the data. In general the more coefficients to be fit, the more data is required. Also when fitting multiple coefficients some of the coefficients are determined with greater precision than others. Thus to get a "good" fit for multiple coefficients a lot more data is required not just the minimum.
−
::If we measure the wind while shooting we can bound and remove a “wind correction” term from that axis. E.g., "Suppose the orthogonal component of wind is ranging at random from 0-10mph during the shooting.  Given lag-time ''t'' this will expand the no-wind horizontal dispersion at the target by <math>\sigma_{wind}</math>."<ref>Wind deflection is a function of the ballistic curve and distance, but can be expressed as a simple product of the cross-wind velocity and lag time. For more information on the "lag rule" see Bryan Litz, ''Applied Ballistics for Long Range Shooting, 2<sup>nd</sup> Edition'' (2011) A4; or Robert McCoy, ''Modern Exterior Ballistics, 2<sup>nd</sup> Edition'' (2012) 7.27.</ref>  Since variances are additive we could adjust <math>\sigma_h</math> via the equation <math>{\sigma'}_h^2 = \sigma_h^2 - \sigma_{wind}^2</math>.
 
−
:(2) The primary source of vertical stringing is muzzle velocity.  
 
−
:: We can actually measure with a chronograph and then correct for that source of variation. E.g., If standard deviation of muzzle velocity is <math>\s_{mv}</math> then, given the bullet's ballistic model for the given target distance, the vertical spread attributable to that is some <math>\s_v</math>.  Here too we can remove this known source of dispersion from our samples via the equation <math>sigma_v^2 = \sigma_v^2 - f(\sigma_{mv}^2</math>.  This adjustment is shown in several of the examples:
 
−
::* [[22LR CCI 40gr HV 40-shot 100-yard Example]]
 
−
::* [[300BLK Subsonic 20-shot 100-yard Example]]
 
  
−
= Four Special Cases for Dispersion =
+
Thus to fit the COI at least two shots are required. To fit the constant for the Rayleigh equation another shot would be required for a total of three shots. To fit the Hoyt distribution an additional five shots would be required for a total of seven shots. Probably 10 shots would be required to get a "decent" fit for the Rayleigh distribution, and at least 25 for the Hoyt distribution.
  
−
Neglecting flyers, and assuming perfect aim, the overall assumptions about shot dispersion result in four cases for statistical analysis.
+
== Notation in Simplified Cases ==
−
 
−
In the four cases below the assumptions use ''approximately equal to'' <math>(\approx)</math>) rather than ''strictly  equal to'' (=). This is an acknowledgement that we are dividing the cases into ones that are close enough to be useful, even though they most certainly are not exact. There is absolutely no method by which the true population values for <math>\bar{h}, \bar{v},\sigma_h</math> and <math>\sigma_v</math> can be determined. We can only get experimental estimates from calculations based on sample data for the factors <math>\mu_h, \mu_v, s_h</math> and <math>s_v</math> and these estimates are at best only good to a scant few significant figures. Thus the difference between ''approximately equal to'' and ''strictly equal to'' is really under experimental control. In other words, we can theoretically make the measurements as precise as we want by collecting more data, but practically there are limits.
 
  
−
The formulas for the distributions are given in terms of the population parameters (i.e. <math>\bar{h}, \bar{v}, \sigma_h, \mbox{and } \sigma_v)</math> rather than the experimentally determined factors (i.e. <math>\mu_h, \mu_v, s_h, \mbox{and } s_v)</math> on purpose to emphasize the theoretical nature of the assumptions. Of course the "true" population parameters are unknown, and we estimate them with the experimentally fitted values about which there is some error.  
+
The formulas for the distributions in the cases detailed in subsequent parts of this page are given in terms of the population parameters (i.e. <math>\mu_h, \mu_v, \sigma_h, \mbox{and } \sigma_v</math>) rather than the experimentally determined factors (i.e. <math>\bar{h}, \bar{v}, s_h, \mbox{and } s_v</math>) on purpose to emphasize the theoretical nature of the assumptions. Of course the "true" population parameters are unknown, and they could only be estimated with the corresponding experimentally fitted values about which there is some error.
  
−
==Case 1, Equal variances and uncorrelated (Rayleigh Distribution) ==  
+
= Conformance Testing =
 +
 
 +
== <math>\rho \approx 0</math> ==
 +
 
 +
only way linear least squares
 +
 
 +
== <math>\sigma_h \approx \sigma_v </math>==
 +
 
 +
# F-Test <math>\frac{s_h^2}{s_v^2}</math>&nbsp;&nbsp;&nbsp;&nbsp; if &nbsp;&nbsp;&nbsp;<math>s_h < s_v</math>&nbsp;&nbsp;&nbsp; else &nbsp;&nbsp;&nbsp;<math>\frac{s_v^2}{s_h^2}</math>
 +
# Studentized Ranges
 +
# Chi-Squared <math>(n-1) \frac{s^2}{\hat{\sigma}^2}</math>
 +
 
 +
= Circular Shot Distribution about COI =
 +
 
 +
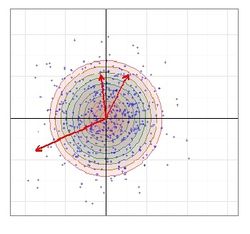
== Case 1, Rayleigh Distribution ==  
 +
[[File:raleigh.jpg|250px|thumb|right| Shots dispersed about the COI. A circular dispersion is the Rayleigh distribution.]]
 
Given: <br />
 
Given: <br />
 
#<math>\sigma_h \approx \sigma_v</math><br />
 
#<math>\sigma_h \approx \sigma_v</math><br />
 
#<math>\rho \approx 0</math><br />
 
#<math>\rho \approx 0</math><br />
 
then the  mathematical formula for the dispersion distribution would be the Rayleigh distribution:<br />
 
then the  mathematical formula for the dispersion distribution would be the Rayleigh distribution:<br />
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>f(r) = \frac{r}{\sigma_{RSD}^2} e^{-r^2/(2\sigma_{RSD}^2)}, \quad r \geq 0,</math> and <math>\sigma_{RSD}</math> is the distribution shape factor known as the Radial Standard Deviation.<br />
+
&nbsp;&nbsp;&nbsp;&nbsp;<math>f(r) = \frac{r}{\Re^2} e^{-r^2/(2\Re^2)}, \quad r \geq 0,</math> and <math>\Re</math> is the shape factor of the Rayleigh distribution.<br />
  
−
This is really the best case for shot dispersion. Shot groups would be round. Strictly, for the Rayleigh distribution to apply, then  <math>\sigma_h = \sigma_v</math>, in which case <math>\sigma_{RSD} = \sigma_h = \sigma_v</math>. For the "loose" application of the Rayleigh distribution to apply, then <math>\sigma_{RSD} \approx (\sigma_h + \sigma_v)/2</math>
+
This is really the best case for shot dispersion. Shot groups would be round.  
  
 +
Strictly, for the Rayleigh distribution to apply, then  <math>\sigma_h = \sigma_v</math>, in which case <math>\Re = \sigma_h = \sigma_v</math>. For the "loose" application of the Rayleigh distribution to apply, then <math>\Re \approx (\sigma_h + \sigma_v)/2 \approx \sqrt{\frac{\sigma_h^2 + \sigma_v^2}{2}}</math>.
  
 
The following statistical measurements are appropriate:
 
The following statistical measurements are appropriate:
 
* Circular Error Probable (CEP)
 
* Circular Error Probable (CEP)
 
* Covering Circle Radius (CCR)
 
* Covering Circle Radius (CCR)
−
* Group Size (GS)  
+
* Diagonal
 +
* Extreme Spread (ES)  
 
* Figure of Merit (FOM)
 
* Figure of Merit (FOM)
 
* Mean Radius (MR)
 
* Mean Radius (MR)
−
* Rayleigh Distribution
+
* Radial Standard deviation
  
−
Notes:
+
'''Notes:'''
−
# In this case that the FOM, and Group Size are different measurements.
+
# The Diagonal, the Extreme Spread and the FOM are different measurements, even though they conceivable could be based on the same two shots! The Extreme Spread would only depend on the two shots most distant in separation. The the Diagonal and the FOM would depend on two to four shots. For a large number of shots we'd typically expect four different shots to define the extremes for horizontal and vertical deflection.
−
# The group size would only depend on the two shots most distant in separation. The FOM would depend on two to four shots. For a large number of shots we'd typically expect four different shots to define the extremes for horizontal and vertical deflection.
+
# For the measures for the CCR, the Diagonal, the GS and the FOM measurements a target would a ragged hole would be acceptable, but for the rest of the measures the {''h,v''} positions of each shot must be known.
−
# For the measures for the CCR, the GS and the FOM measurements a target would a ragged hole would be acceptable, but for the rest of the measures the {''h,v''} positions of each shot must be known.
+
# Experimentally the radial distance for each shot, ''i'', is <math>r_i = \sqrt{(h_i - \bar{h})^2 + (v_i - \bar{v})^2}</math>
−
# Experimentally the radial distance for each shot, ''i'', is <math>r_i = \sqrt{(h_i - \mu_h)^2 + (v_i - \mu_v)^2}</math>
 
 
# The conversion to polar coordinates results in each shot having coordinates <math>(r, \theta)</math>. (a) The conversion implicitly assumes that the polar coordinates have been translated so that the center is at the Cartesian Coordinate of the true center of the population <math>(\bar{h}, \bar{v})</math>. (b) The distribution of <math>\theta</math> is assumed to be entirely random and hence irrelevant. This assumption is testable. (c) The distribution is thus converted from a two-variable distribution to a one-variable distribution.
 
# The conversion to polar coordinates results in each shot having coordinates <math>(r, \theta)</math>. (a) The conversion implicitly assumes that the polar coordinates have been translated so that the center is at the Cartesian Coordinate of the true center of the population <math>(\bar{h}, \bar{v})</math>. (b) The distribution of <math>\theta</math> is assumed to be entirely random and hence irrelevant. This assumption is testable. (c) The distribution is thus converted from a two-variable distribution to a one-variable distribution.
  
−
==Case 2, Equal variances and correlated ==  
+
{| class="wikitable"
 +
| [[File:Bullseye.jpg|50px]] Note that there is a conundrum in how we are "averaging" the horizontal and vertical standard deviations to get <math>\sigma_{\Re}</math>. Look at the two expressions. They lead to two choices, either of which may casually seem valid.
 +
* <math>\sigma_h = \sigma_v</math>
 +
* <math>\sigma_h^2 = \sigma_v^2</math>
 +
 
 +
In general if we look at the first formula "averaging" it leads to using:<br />
 +
 
 +
&nbsp;&nbsp;&nbsp;<math>\Re = \frac{\sigma_h + \sigma_v}{2} = \sigma_h</math> &nbsp;&nbsp;(with substituting <math>\sigma_h</math> for <math>\sigma_v</math>)
 +
 
 +
However in statistics standard deviations are "averaged" (pooled) by taking the square root of the average of their variances:<br />
 +
&nbsp;&nbsp;&nbsp;<math>\Re^2 = {\frac{\sigma_h^2 + \sigma_v^2}{2}}</math><br />
 +
&nbsp;&nbsp;&nbsp;<math>\Re = \sqrt{\frac{\sigma_h^2 + \sigma_v^2}{2}} = \sigma_h </math>&nbsp;&nbsp;(with substituting <math>\sigma_h</math> for <math>\sigma_v</math>)
 +
 
 +
but:
 +
 
 +
&nbsp;&nbsp;&nbsp;<math>\frac{\sigma_h + \sigma_v}{2} = \sqrt{\frac{\sigma_h^2 + \sigma_v^2}{2}}</math>
 +
&nbsp;&nbsp;if and only if <math>\sigma_h \equiv \sigma_v</math>
 +
 
 +
Thus we should take the extent that:
 +
 
 +
&nbsp;&nbsp;&nbsp;<math>\frac{\sigma_h + \sigma_v}{2} \neq \sqrt{\frac{\sigma_h^2 + \sigma_v^2}{2}}</math>
 +
 
 +
as a severe warning that we can not push the assumption that <math>\sigma_h \approx \sigma_v</math> too far if we expect the simplification of the general Hoyt distribution to the Rayleigh distribution to give meaningful results.
 +
 
 +
The situation is even more tenuous given the small samples that shooters typically use. In general the relative precision of the variance value about a mean is much less precise than the relative precision of the mean value. The statistical test to compare two experimental variance values (i.e. <math>\sigma_h^2, \text{and} \sigma_v^2</math> in our case) is the F-Test which uses the ratios of the variances. For small samples a large difference would need to be observed before the ratio would be statistically significantly because of the imprecision in the individual experimental variance values.
 +
|}
 +
 
 +
= Elliptical Shot Distribution about COI =
 +
 
 +
== Case 2, Equal variances and correlated ==  
 
Given:<br />
 
Given:<br />
 
#<math>\sigma_h \approx \sigma_v</math><br />
 
#<math>\sigma_h \approx \sigma_v</math><br />
Line 104: Line 205:
 
* Elliptic Error Probable
 
* Elliptic Error Probable
  
−
==Case 3, Unequal variances and uncorrelated ==  
+
==Case 3, Unequal variances and uncorrelated (Orthogonal Elliptical Distribution)==  
 
Given:<br />  
 
Given:<br />  
 
# <math>\sigma_h \neq \sigma_v</math><br />
 
# <math>\sigma_h \neq \sigma_v</math><br />
Line 120: Line 221:
 
       \right)
 
       \right)
 
   </math>
 
   </math>
 +
For the purposes of this wiki, this distribution will be called the '''Orthogonal Elliptical Distribution'''. It is obviously a special case of the Hoyt distribution which in turn is a special case of the bivariate normal distribution.
  
−
The following statistical measurements are appropriate:
+
In order of the model complexity, the following statistical measurements are appropriate:
−
* Diagonal
 
 
* Individual Horizontal and Vertical variances
 
* Individual Horizontal and Vertical variances
 +
* Elliptic Error Probable
  
 
In this case the horizontal and vertical standard deviations could be determined independently from the horizontal and vertical measurements respectively.
 
In this case the horizontal and vertical standard deviations could be determined independently from the horizontal and vertical measurements respectively.
  
−
==Case 4, Unequal variances and correlated ( General Bivariate Distribution)==  
+
==Case 4, Unequal variances and correlated (Hoyt Distribution)==  
 +
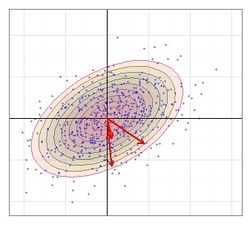
[[File:Hoyt.jpg|250px|thumb|right| Hoyt Distribution - Shots dispersed about COI in an elliptical pattern which has its major axis at an angle to the coordinate axes.]]
 +
 
 
Given:<br />  
 
Given:<br />  
 
#<math>\sigma_h \neq \sigma_v</math><br />
 
#<math>\sigma_h \neq \sigma_v</math><br />
 
#<math>\rho \neq 0</math><br />
 
#<math>\rho \neq 0</math><br />
 
# The {''h,v''} position of each shot must be known.  
 
# The {''h,v''} position of each shot must be known.  
−
then the mathematical formula for the dispersion distribution would be:<br />
+
then the mathematical formula for the dispersion distribution would be the Hoyt distribution with no simplifications:<br />
 
&nbsp;&nbsp;&nbsp;&nbsp;<math>
 
&nbsp;&nbsp;&nbsp;&nbsp;<math>
 
     f(h,v) =
 
     f(h,v) =
Line 145: Line 249:
 
   </math>
 
   </math>
  
−
This mathematical formula will be called the ''General Bivariate Gaussian distribution''. This is really the most complex case for shot dispersion. Shot groups would be elliptical or egg-shaped.
+
Shot groups would be elliptical or egg-shaped if either the horizontal range or vertical range were large. The following statistical measurements are appropriate:
−
 
+
* Elliptic Error Probable
−
== Measuring Precision ==
 
−
 
 
−
The following text considers mainly shots from a direct fire weapon firing a single projectile on a vertical
 
−
target within the line of sight, for example rifle or pistol shots. Such weapons as shotguns, intercontinental
 
−
missiles, and motars would have some similar characteristics, but also have factors that are neglected in the
 
−
measurements.
 
−
 
 
−
= Dispersion Units =
 
−
 
 
−
When we talk about shooting precision we are referring to the amount of dispersion we expect to see of each
 
−
shot about a center point (which shooters adjust to match the point of aim).  There are two basic categories of units for
 
−
dispersion, linear distances and as an angle.
 
−
 
 
−
''Linear distance'' typically uses a fixed (and specified) distance. For example the inches in diameter of a
 
−
group of shots at 100 yards.
 
−
 
 
−
''[[Angular Size]]'' is another common unit and is the angle at the tip of the ''cone of fire'' since this is
 
−
independent of the distance at which a target is shot.  The higher the precision, the tighter the cone and hence the smaller the angle at its tip.
 
−
 
 
−
== Linear Distance ==
 
−
 
 
−
In countries using the metric system the extreme spread of shots (group size) would typically be measured in
 
−
centimeters (cm), or perhaps millimeters (mm). Countries (i.e. the USA) still using the British Imperial system
 
−
would typically measure linear distances in inches.
 
−
 
 
−
=== Mil ===
 
−
The other common linear unit is the '''mil''', which simply means thousandth.  For example, '''at 100 yards a
 
−
mil is 100 yards / 1000 = 3.6"'''.  Some more benign confusion also persists around this term, with some
 
−
assuming "mil" is short for milliradian, which is an angular unit.  Fortunately, a milliradian &mdash; 3600"
 
−
tan (1/1000 radians) ≈ 3.600001" inches at 100 yards &mdash; is almost exactly equal to a mil so there’s little
 
−
harm in interchanging ''mil'', ''mrad'', ''milrad'', and ''milliradian''.
 
−
 
 
−
<!--
 
−
    Note also: Even '''mil''' is encumbered by some historical ambiguity. For example,
 
−
    western militaries going  back at least a century used an angular unit for artillery
 
−
    calculations that divided the circle into 6400 "mils," which persists the "NATO mil."
 
−
 
 
−
    [http://en.wikipedia.org/wiki/Angular_mil#Definitions_of_the_angular_mil]
 
−
-->
 
−
 
 
−
== Angular Size ==
 
−
 
 
−
The overall assumption is that the 2-dimensional precision is like a cone that projects linearly from the
 
−
muzzle of the gun -  i.e., double the distance and the dispersion also doubles.  In many instances this model is sufficient. In reality this isn't true for all cases. 
 
−
 
 
−
For example due to projectile spin and aerodynamics there is some point at which a projectile's flight would degrade
 
−
faster than the linear distance. So a 1 inch group at 100 yards might become a 10 inch group at 500 yards, and
 
−
a three foot group at 1000 yards.
 
−
 
 
−
Another example is given by cases documented where a projectile "goes to sleep." Essentially the violent exit of the
 
−
projectile from the muzzle results in an projectile instability which is damped by air resistance. In this
 
−
case a group might be 0.5 inches at 50 yards, but just 3/4 of an inch at 100 yards. Thus the linear group size at a
 
−
longer distance is larger, but not geometrically larger. Note however that if you were using an angular
 
−
measure, then the group size would be smaller at 100 yards than 50 yards.
 
−
 
 
−
=== Minute Of Arc ===
 
−
 
 
−
One of two popular angular units used by shooters is '''MOA''', though there is some ambiguity in this term.
 
−
From high school geometry a circle is divided into 360 degrees, and each degree is divided into 60 minutes. 
 
−
Thus MOA was initially short for Minute of Arc, or arc minute, which is one sixtieth of one degree. 
 
−
 
 
−
'''At 100 yards (3600 inches) one MOA is 3600" tan (1/60 degrees) = 1.047"'''. 
 
−
 
 
−
=== Shooter's Minute of Angle===
 
−
At some point shooters began to expand the acronym as Minute of Angle.  They also rounded its correct value to
 
−
1” at 100 yards, though for clarity the latter unit is properly called "Shooters MOA," or '''SMOA'''.
 
−
 
 
−
 
 
−
== Conversions between measuring units==
 
−
 
 
−
See [[Angular Size]] for detailed illustrations and conversion formulas.
 
−
 
 
−
= Dispersion Measures =
 
−
[[File:SCAR17 150gr 100yd.png|365px|thumb|right|Precision Measures diagrammed on a 10-shot 100-yard group. 
 
−
 
 
−
Data in [[Media:SCAR17_150gr_100yd.xls]]]]
 
−
Nine different measures have been used to characterize the dispersion of bullet holes in a sample target. 
 
−
 
 
−
Some are easier to calculate than others.
 
−
 
 
−
In the following formulas assume that:
 
−
# We are looking at a target reflecting ''n'' shots
 
−
# We are able to determine the center coordinates ''h'' and ''v'' as needed for analysis. For example for
 
−
extreme spread we just need to be able to measure the distance between the two widest shots, but for the
 
−
radial standard deviation we need the horizontal and vertical positions of each shot on the target.
 
−
 
 
−
Some additional mathematical symbols and variables:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;''NSPG'' - Number of Shots Per Group<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\mu_h</math> is defined as <math>\mu_h \equiv \sum_{i=1}^n h_i / n</math><br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\mu_v</math> is defined as <math>\mu_v \equiv \sum_{i=1}^n v_i / n</math>
 
−
 
 
−
== NSPG Invariant Measures ==
 
−
It is worth noting that following measures in this section do not increase with the number of shots per group (NSPG).
 
−
That means that more shots tightens the precision of the measurement but doesn't change its expected value.
 
−
 
 
−
* Mean Radius
 
−
* Circular Error Probable
 
−
* Horizontal and Vertical Variances
 
−
* Radial Standard Deviation of the Rayleigh Distribution
 
−
* Bivariate Gaussian Distribution Parameters
 
−
 
 
−
=== Mean Radius (MR) ===
 
−
The Mean Radius is the average distance over all shots to the groups center.
 
−
 
 
−
{| class="wikitable" class="wikitable" style="font-size:&nbsp;"
 
−
|-
 
−
!
 
−
!
 
−
|-
 
−
| Assumptions
 
−
|
 
−
* Rayleigh Distribution for Shots
 
−
** <math>\sigma_h = \sigma_v</math>
 
−
**<math>\rho = 0</math>
 
−
* No Flyers
 
−
|-
 
−
| Experimental Measure
 
−
| <math>\bar{r} = \sum_{i=1}^n r_i / n</math><br />
 
−
&nbsp;&nbsp;&nbsp; where <math>r_i = \sqrt{(h_i - \mu_h)^2 + (v_i - \mu_v)^2}</math>
 
−
|-
 
−
| PDF
 
−
|
 
−
|-
 
−
| Mode of PDF
 
−
|
 
−
|-
 
−
| Median of PDF
 
−
|
 
−
|-
 
−
| Mean of PDF
 
−
|
 
−
|-
 
−
| CDF
 
−
|
 
−
|-
 
−
| Variables in PDF &amp; CDF
 
−
| <math>r</math>
 
−
|-
 
−
| Fitted parameters
 
−
| <math>\mu_h, \mu_v</math>
 
−
|-
 
−
| (h,v) for all points?
 
−
| Yes
 
−
|-
 
−
| Symmetric about Measure?
 
−
| No, but the distribution will become more symmetric  as the number of shots in a group increases.
 
−
|-
 
−
| NSPG Invariant
 
−
| Yes
 
−
|}
 
−
Formula:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\bar{r} = \sum_{i=1}^n r_i / n</math> where <math>r_i = \sqrt{(h_i - \mu_h)^2 + (v_i - \mu_v)^2}</math>
 
−
 
 
−
As we will see in [[Closed Form Precision]], the Mean Radius is typically only 6% larger than the Circular
 
−
Error Probable.  Since this is within the margin of error of most real-world usage the terms MR and CEP may be
 
−
interchanged in casual usage.
 
−
 
 
−
=== [[Circular Error Probable]] (CEP) ===
 
−
<math>CEP_p</math>, for <math>p \in [0, 1)</math>, is the radius of the smallest circle that covers proportion ''p'' of the shot group.  When ''p'' is not indicated it is assumed to be <math>CEP_{0.5}</math>, which is the ''median shot radius'' (50% radius).
 
−
 
 
−
=== Horizontal and Vertical Variances ===
 
−
 
 
−
Assumptions:
 
−
* <math>\sigma_h \neq \sigma_v</math>
 
−
* <math>\rho = 0</math>
 
−
* No Flyers
 
−
 
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\sigma_h^2 = \frac{\sum^{n}(h_i - \bar{h})^2}{n - 1}, \quad \sigma_v^2 = \frac{\sum^{n}(v_i - \bar{v})^2}{n - 1}</math>
 
−
 
 
−
Often these will be given as standard deviations, which is just the square root of variance.
 
−
 
 
−
=== Radial Standard Deviation of the Rayleigh Distribution ===
 
−
 
 
−
From high school mathematics one should remember the two coordinate systems - Cartesian Coordinates
 
−
and Polar Coordinates. Essentially the Rayleigh distribution converts shots from the Cartesian
 
−
Coordinate system to the Polar Coordinate system. It is implicit in the coordinate conversion that the origin
 
−
for the polar coordinate system is at the average point of impact.  Thus for the polar coordinates the radial positioon of each shot will be relative to origin, or the average point of impact. Each shot will then have two coordinates, an angle, <math>\theta, </math> and the radius, ''r''. Given that the shot distribution assumptions hold, then the angle should be entirely random and is of no interest. The two-variable problem has thus been reduced to a one-variable problem of determining the distribution for the shot radius.
 
−
 
 
−
Given that the conversion for the radial distance for each shot ''i'' from Cartesian Coordinates is:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>r_i = \sqrt{(h_i - \bar{h})^2 + (v_i - \bar{v})^2}</math><br />
 
−
then the mean radius for the sample of i shots can be calculated in a straight forward manner using:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\bar{r} = \frac{\sum_{i=1}^n r_i}{n}</math><br />
 
−
and likewise for the standard deviation of the radius sample:<br>
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>s_r = \sqrt{\frac{\sum^{n}(r_i - \bar{r})^2}{n - 1}}</math><br />
 
−
 
 
−
Now assuming that the shot dispersion follows the Bivariate Gaussian Distribution and that the following simplifying assumptions are true:<br />
 
−
* <math>\sigma_h = \sigma_v</math>
 
−
* <math>\rho = 0</math>
 
−
* No Flyers
 
−
then the equation for the PDF for an individual shot is given by the Rayleigh distribution function which is:<br>
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>f(r) = \frac{r}{\sigma_{RSD}^2} e^{-r^2/2\sigma_{RSD}^2)}, \quad r \geq 0,</math><br />
 
−
where <math>\sigma_{RSD}</math> is the single scale parameter of the distribution and is called the '''Radial Standard Deviation'''. Solving the distribution function for the mean radius and the standard deviation of the radius shows that they both are a proportional to <math>\sigma_{RSD}</math>.
 
−
 
 
−
For the mean radius:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\bar{r} = \sqrt{\pi/2} \sigma_{RSD} \approx 1.2533 \sigma_{RSD}</math><br />
 
−
and for the standard deviation of the radius:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\sigma_r = \sqrt{\frac{4 - \pi}{2}} \sigma_{RSD} \approx 0.6551 \sigma_{RSD}</math><br />
 
−
 
 
−
There is an additional association which needs to be mentioned. Given the assumption <math>\sigma_h = \sigma_v</math>, then according to the strict derivation of the Rayleigh distribution, <math>\sigma_{RSD} = \sigma_h = \sigma_v</math>. In reality for the sample of shots <math>s_h \approx s_v</math> which means that <math>s_{RSD} = (s_h + s_v)/2</math>
 
−
 
 
−
This bit of mathematical magic is due to the fact that the error of a shot from the polar origin has been
 
−
broken into two parts, an angular error and a radial error. The implicit assumption here is that the angular
 
−
part of the error is entirely random and hence not significant in characterizing the distribution of the radius.
 
−
Thus that part of the error in a shot's position has been isolated and removed. This mathematical manipulation isn't "free." The essence is that the Rayleigh model places an even greater dependency on the assumptions when making predictions about confidence intervals which use the  standard deviation. In plainer language if the assumptions don't hold, then a small error in the estimated <math>\sigma_{RSD}</math> results in larger errors in the confidence interval predictions.
 
−
 
 
−
=== Bivariate Gaussian Distribution Parameters ===
 
−
 
 
−
Assumptions:
 
−
* Full Bivariate Gaussian Distribution for shot dispersion
 
−
** <math>\sigma_h \neq \sigma_v</math>
 
−
** <math>\rho \neq 0</math>
 
−
* No Flyers
 
−
The full bivariate Gaussian distribution is:<br >
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>
 
−
    f(h,v) =
 
−
      \frac{1}{2 \pi  \sigma_h \sigma_v \sqrt{1-\rho^2}}
 
−
      \exp\left(
 
−
        -\frac{1}{2(1-\rho^2)}\left[
 
−
          \frac{(h-\bar{h})^2}{\sigma_h^2} +
 
−
          \frac{(v-\bar{v})^2}{\sigma_v^2} -
 
−
          \frac{2\rho(x-\bar{h})(y-\bar{v})}{\sigma_h \sigma_v}
 
−
        \right]
 
−
      \right),
 
−
  </math>
 
−
 
 
−
In general case, when <math>\sigma_h \neq \sigma_v</math>, then the actual standard deviation
 
−
of the radius <math>r_i</math> is not easy to calculate and is given by the formula:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>\frac{\sigma_h^2}{\pi} (\pi - 2 K^2(1 - \frac{\sigma_v^2}{\sigma_h^2})) + \sigma_v^2</math>
 
−
where ''K'' is the complete elliptic integral.
 
−
 
 
−
== NSPG Variant Measures ==
 
−
 
 
−
The following measures in this section do increase with group size.  They are more commonly used because they
 
−
are obtained by direct measurements with either no calculations, or very simple calculations. But they are
 
−
statistically weaker because they mostly ignore inner data points.
 
−
* Group Size (GS)
 
−
* Diagonal (D)
 
−
* Figure of Merit (FOM)
 
−
* Covering Circle Radius (CCR)
 
−
 
 
−
In general a ragged hole does not present a problem for these measures. However a ragged hole might be an
 
−
experimental problem depending, for example, if the projectile style does not cut relatively clean holes, or if the target
 
−
tears.
 
−
 
 
−
=== Group Size (GS) ===
 
−
The Group Size is is the largest center-to-center distance between any two points, ''i'' and ''j'', in the group. It is often
 
−
called the Extreme Spread in the statistical literature.
 
−
 
 
−
Assumptions:
 
−
* Rayleigh Distribution for shot dispersion
 
−
** <math>\sigma_h = \sigma_v</math>
 
−
** <math>\rho = 0</math>
 
−
* No Flyers
 
−
 
 
−
Formula:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>ES = \max \sqrt{(h_i - h_j)^2 - (v_i - v_j)^2)}</math>
 
−
 
 
−
'''Note:''' Be careful with with the phrase ''extreme spread''. Shooters will often refer to the range of
 
−
values from a chronograph as the ''extreme spread''. Context should allow an easy determination of the correct meaning of the phrase. 
 
−
 
 
−
=== Diagonal (D) ===
 
−
The Diagonal is the length of the diagonal line through the smallest rectangle covering the sample group. Note
 
−
that it is implicit that the rectangle is oriented along the horizontal and vertical axes. The diagonal may be
 
−
determined by two to four points depending on the pattern of shots within the group.
 
−
 
 
−
Assumptions:
 
−
* <math>\sigma_h \neq \sigma_v</math>
 
−
* <math>\rho = 0</math>
 
−
* No Flyers
 
−
 
 
−
Formula:<br />
 
−
<math>ES = \sqrt{(h<sub>high</sub> - h<sub>low</sub>)^2 - (v<sub>high</sub> - v<sub>low</sub>)^2)}</math>
 
−
where <math>(h<sub>high</sub> - h<sub>low</sub>)</math> and <math>(v<sub>high</sub> - v<sub>low</sub>)</math> are the observed horizontal and vertcal ranges respecively.
 
−
 
 
−
=== Figure of Merit (FOM) ===
 
−
 
 
−
The Figure of Merit is the average extreme width and height of the group. The FOM may be determined by
 
−
two to four points depending on the pattern within the group.
 
−
 
 
−
Assumptions:
 
−
* Rayleigh Distribution for shot dispersion
 
−
** <math>\sigma_h = \sigma_v</math>
 
−
** <math>\rho = 0</math>
 
−
* No Flyers
 
−
 
 
−
Formula:<br />
 
−
&nbsp;&nbsp;&nbsp;&nbsp;<math>ES = ((h_{high} - h_{low}) + (v_{high} - v_{low})) / 2</math>
 
−
 
 
−
The FOM would be reasonable when <math>\sigma_h \approx \sigma_v</math>. However if it is known that <math>\sigma_h \ne \sigma_v</math>, then using the measurement makes no sense. It would be better to use the Diagonal measurement.
 
−
 
 
−
=== Covering Circle Radius (CCR) ===
 
−
 
 
−
The Covering Circle Radius is the radius of the smallest circle containing all shot centers.  This will
 
−
pass through at least the two extreme shots (in which case CCR = (Group Size) / 2 ) or at most it will pass
 
−
through three outside shots.
 
−
 
 
−
Assumptions:
 
−
* Rayleigh Distribution for shot dispersion
 
−
** <math>\sigma_h = \sigma_v</math>
 
−
** <math>\rho = 0</math>
 
−
* No Flyers
 
−
 
 
−
 
 
−
= Which Measure is Best? =
 
−
 
 
−
[[Precision Models]] discusses in more detail the assumptions about shot dispersion. The disconcerting truth is that there is no ''universally best measurement''. All measurements are dependent on assumptions about the "true" distribution for the dispersion of  individual shots, and about the presence of true "outliers" in the data. In practice the effect of neither of these factors is known.
 
−
 
 
−
The lack of an absolute truth may be mitigated with an expectation of picking reasonable assumptions and a mathematical
 
−
model that is ''good enough''. In essence start with a simple assumptions and model, and if the data indicates that the assumptions or model are inadequate, then increase the complexity of the model. Here complexity of the model essentially means the
 
−
number of parameters which are determined experimentally. So the Rayleigh model has three experimental
 
−
parameters (average horizontal position, average vertical position and the standard deviation of the radius),
 
−
but the full bivariate Gaussian distribution has five ((average horizontal position, average vertical position,
 
−
the horizontal standard deviation, the vertical standard deviation and ρ). The drawback here is that since the
 
−
full bivariate Gaussian distribution has more parameters to fit experimentally, it would require more data to
 
−
obtain a good experimental fit.
 
−
 
 
−
Shooters use the term ''flyer'' to denote the statistical term ''outlier''. An outlier denotes an expected
 
−
"good shot" with an abnormally large dispersion. So a shot that is much father than average from the center of the group would be a flyer. On the other hand, let's assume that the shooter realizes
 
−
that his rifle was canted as the rifle discharges. The shooter would call that a "bad shot" before
 
−
determining the shot position and would ignore that shot when making his measurements regardless of where
 
−
the projectile landed.
 
−
 
 
−
It is convenient to consider the Rayleigh distribution function (or the full bivariate Gaussian as appropriate)
 
−
as the gold standard given the situation that the underlying assumptions about shot dispersion and the
 
−
lack of outliers holds. In this situation the Rayleigh model is 100% efficient since it makes as much use
 
−
of the statistical data as is theoretically possible. In statistics the standard deviation of a measurement divided by the measurement expresses the error as a dimensionless per centage. The effiency of various measures can be thus compared by using the ratios of the variances, the relative standard deviations squared.
 
−
 
 
−
However one must be careful to not be too swayed by theory as opposed to experimental reality. In reality the
 
−
conformance to theory is only due to a lack of enough experimental data to infer that the theory is incorrect.
 
−
Also for the Rayleigh model neither the position of the center, nor the average radius, nor the standard
 
−
deviation of the radius are [[http://en.wikipedia.org/wiki/Robust_statistics robust estimators]].
 
−
 
 
−
= Examples =
 
  
−
One of the important questions addressed here is ''what'' to measure in order to determine the intrinsic
+
= Related topics =
−
precision of a shooting system, and what sample size is sufficient to achieve any degree of statistical
 
−
significance.
 
  
−
Following are common measurements used by shooters or in the firearm industry:
+
See also the following topics which are closely related:
−
* [[Extreme Spread]] of one 3-shot group, usually at 100 yards.
+
* [[Error Propagation]] - A basic discussion of how errors propagate when making measurements.   
−
::This is statistically poor, especially when there is no reference to how many 3-shot groups were sampled.
+
* [[Stringing]] - Definition of stringing and how it can be handled
−
::([[http://www.ar15.com/mobile/topic.html?b=3&f=118&t=279218|An extended practical, and amusing, critique of the 3-shot group is archived here]].)
 
−
* Extreme Spread of one 5-shot group, sometimes excluding the worst shot.  Hardly any better.
 
−
* Average, Max, and Min Extreme Spread of five 5-shot groups. 
 
−
::([[Range_Statistics#Example:_NRA.27s_Test_Protocol|This is the protocol used by the NRA's magazines and is
 
−
actually rather efficient]].)
 
−
* The US Army Marksmanship Unit at Ft. Benning, GA uses a minimum of 3 consecutive 10-shot groups fired with the rifle in a machine rest when testing service rifles.  Armed forces also often explicitly uses the more statistically powerful Mean Radius and Circular Error Probable measures.
 
−
<!--
 
−
    Not sure about the applicability of these examples, but I'll leave them in for now since
 
−
    they were from an earlier version of this text.
 
−
-->
 
  
 
= References =
 
= References =

Latest revision as of 12:05, 20 June 2015

Before considering the measurements that will be used for the actual statistical analysis, let's consider the assumptions about projectile dispersion about the Center of Impact (COI) and how sets of those assumptions might be grouped into different classifications. The various classifications will offer insight as to the fundamental patterns expected for shots and insights to the interactions of various measures. Thus an understanding of the basic assumptions about projectile dispersion is key in being able to effectively use the measures.

The COI is the only true point of reference which can be calculated from the pattern of shots on a target. Thus the COI is the reference point for precision measurements. The overall error that we are interested in measuring is the sum of all the various interactions that make multiple projectiles shot to the same point of aim (POA) disperse about the COI.

Since we are primarily interested in the dispersion relative to the COI, the overall assumption is that the weapon could be properly sighted so that the COI would be the same as the POA. In practice this is achieved by adjusting the weapon's sights. Thus in order to isolate projectile dispersion, all of the factors of internal and external ballistics that cause a bias to the COI on a target will be ignored. For example, for the purposes of classifying projectile dispersion, accuracy errors due to POA errors will be ignored.

The Normal distribution is the broadly assumed probability model used for a single random variable and it is characterized by its mean \((\bar{x})\) and standard deviation \((\sigma)\). The central limit theorem shows that for measures for the "average" shot, or averages of multiple targets are used, then for "large" samples the averages will conform to Normal distribution even if the fundamental distribution is not a normal distribution.

Distribution of samples from a symmetric bivariate normal distribution. Axis units are multiples of σ.

Since we are interested in shot dispersion on a two-dimensional target we will assume that the horizontal and vertical dispersions of the population of shots are each Normal distributions. Thus the horizontal dispersion will have mean \(\mu_H\) and standard deviation \(\sigma_H\). The vertical dispersion will have mean \(\mu_V\) and standard deviation \(\sigma_V\). Then a further assumption is made by assuming that the two dimensional expansion of the Normal distribution the Bivariate Normal distribution, applies. This adds an additional term the correlation parameter ρ. (See also: What is ρ in the Bivariate Normal distribution?) Thus the expectation is that distribution should then describe, the dispersion of a gunshots about the COI, (\(\mu_H\) and \(\mu_V\)). The full bivariate normal distribution is thus:
    \( f(H,V; \mu_H, \mu_V, \sigma_H, \sigma_V, \rho) = \frac{1}{2 \pi \sigma_H \sigma_V \sqrt{1-\rho^2}} \exp\left( -\frac{1}{2(1-\rho^2)}\left[ \frac{(H-\mu_H)^2}{\sigma_H^2} + \frac{(V-\mu_V)^2}{\sigma_V^2} - \frac{2\rho(H-\mu_H)(V-\mu_V)}{\sigma_H \sigma_V} \right] \right) \)

where:
    \(-1 ≤ \rho ≤ 1\)
    \( \sigma_H>0 \) and \( \sigma_V>0 \)

Note that the above restrictions are not additional restrictions on the model, but rather simply pointing out how the mathematics works. Thus they are more analogous to the mathematical notion that a person can't have a negative age.

Bullseye.jpg An ancillary point worth mentioning is that the assuming the Normal distribution in three dimensions leads to the Maxwell–Boltzmann distribution which is the foundation of the ideal gas laws.

Simplification of the Hoyt distribution into Special Cases

To eliminate the COI (\(\mu_H\), \(\mu_V\)) which makes the equations "messier", a translation of the coordinate system to the COI is desired. Thus:

    \(\mu_h = 0\)   and    \(\mu_v = 0\)

    \(h = H - \mu_H\)   and    \(v = V - \mu_V\)

    and  \(\sigma_h = \sigma_H \)   and   \(\sigma_v = \sigma_V \)

This is a very pragmatic and justifiable consideration since the COI can be measured on the target, and the dispersion about the COI is the aspect of interest when measuring precision. As noted before, by adjusting the weapon's sights the POA can be made to coincide with the COI. Thus this simplification of the dispersion equations is strictly for ease of understanding as is not a limitation on the nature of the dispersion classifications. With the translation of the coordinate system to the COI, then the general bivariate normal equation becomes the Hoyt distribution:
    \( f(h,v; \sigma_h, \sigma_v, \rho) = \frac{1}{2 \pi \sigma_h \sigma_v \sqrt{1-\rho^2}} \exp\left( -\frac{1}{2(1-\rho^2)}\left[ \frac{h^2}{\sigma_h^2} + \frac{v^2}{\sigma_v^2} - \frac{2\rho hv}{\sigma_h \sigma_v} \right] \right) \)

Looking at this equation two other different mutually exclusive simplifications can be readily seen:

  • Either \(\sigma_h = \sigma_v\) (equal standard deviations) or \(\sigma_h \neq \sigma_v\) (unequal standard deviations).
Obviously if we could measure both \(\sigma_h\) and \(\sigma_v\) with a very high precision (e.g 6 significant figures), then the two quantities would never really be equal. But in many cases the assumption is reasonable. In reality since shooters typically collect only a small amount of data, statistical tests will fail to detect a difference unless the difference is great. In such cases the shot pattern would be noticeably elliptical, not round.
  • Either \(\rho = 0\) (uncorrelated) or \(\rho \neq 0\) (correlated).
Bullseye.jpg: !! CAREFUL !! Correlation does not imply causation
There is somewhat famous example. A researcher gathered statistics for stork sightings and births in a particular county over a twenty year period. Analysis of the data showed that over the twenty year period both stork sightings and births had increased with a very significant linear correlation. From the data you might erroneously infer that storks do bring babies!

The pair of mutually exclusive assumptions thus results in four cases for analytical evaluation as shown in the Table below. There is one case that results in circular groups, and three that result in elliptical groups. As the different in variances gets greater, or the further \(\rho\) is from 0, then the ellipse will be more pronounced.

Group Shape vs. Assumptions (COI at Origin)
\(\sigma_h \approx \sigma_v\) \(\sigma_h \neq \sigma_v\)
\(\rho \approx 0\) Case 1 - Circular Groups
  • special case is the Rayleigh Distribution
  • Parameter(s) to fit (other than COI):
- \(\sigma_{\Re}\) (pooled value of \(\sigma_h\) and \(\sigma_v\))
 Case 3 - Elliptical Groups
  • special case is the Orthogonal Elliptical Distribution
  • Major axis of ellipse along
    horizontal or vertical axis
  • Parameter(s) to fit (other than COI):
- \(\sigma_h\)
- \(\sigma_v\)
\(\rho \neq 0\)
  • Major axis of ellipse at an angle to
    both the horizontal and vertical axes
 Case 2- Elliptical Groups
  • Parameter(s) to fit (other than COI):
- \(\sigma_{\Re}\) (pooled value of \(\sigma_h\) and \(\sigma_v\))
- \(\rho\)
 Case 4 - Elliptical Groups
  • general case of the Hoyt distribution required
  • Parameter(s) to fit (other than COI):
- \(\sigma_h\)
- \(\sigma_v\)
- \(\rho\)

Experimental reality of Comparing \(s_h\) and \(s_v\)

The table above uses approximately equal to \((\approx)\) rather than strictly equal to \(( = )\). This is an acknowledgement that we are dividing the cases into ones that are close enough to be useful, even though they most certainly are not exact. To be overly persnickety there are two considerations.

First we can only get experimental estimates from calculations based on sample data for the factors \(\sigma_h\), \(\sigma_v\), \(\rho\) and these estimates are at best only good to a scant few significant figures. Thus even though the difference between approximately equal to and strictly equal to is under some experimental control there are practical limits. In other words, we can theoretically make the measurements as precise as we want by collecting more data, but it is quickly impractical to do so. (Assume that to double the precision that we have to quadruple the sample size. This exponential increase quickly becomes unmanageable. It is easy to pontificate about averaging over a million targets, but no one is going to shoot that many.) Thus even if \(\sigma_h \equiv \sigma_v\) we'd never expect that we'd experimentally get \(s_h = s_v\) due to experimental error.

Second there is the good enough. Shooting by definition is going to have fairly small sample sizes. So if \(0.66s_h < s_v < 1.5 s_h\) then, as a rule of thumb, that is probably good enough. Of course for large sample we would want to tighten the window. The harsh reality is that if \(s_h\) and \(s_v\) could be measured with great precision (e.g. to ten significant figures), then two values would always be statistically significantly different.

Thus the approximation that \(\sigma_h \approx \sigma_v\) will be used unless the variances are known to be statistically significantly different. On the experimental data it is possible to test for a statistically significant difference by using a ratio of \(s_h^2\) and \(s_v^2\) via the F-Test. The "catch" in using the F test is that the variance has poor precision for small samples. Thus the difference must be great for the F-Test to detect that the two variances are not equal.

Simplifications Reduce Number of Coefficients to Fit

The Hoyt distribution is general enough to be able to fit all four of the special cases in the table above. The point in making special cases of the Hoyt distribution is to reduce the number of coefficients to fit to the data. In general the more coefficients to be fit, the more data is required. Also when fitting multiple coefficients some of the coefficients are determined with greater precision than others. Thus to get a "good" fit for multiple coefficients a lot more data is required not just the minimum.

Thus to fit the COI at least two shots are required. To fit the constant for the Rayleigh equation another shot would be required for a total of three shots. To fit the Hoyt distribution an additional five shots would be required for a total of seven shots. Probably 10 shots would be required to get a "decent" fit for the Rayleigh distribution, and at least 25 for the Hoyt distribution.

Notation in Simplified Cases

The formulas for the distributions in the cases detailed in subsequent parts of this page are given in terms of the population parameters (i.e. \(\mu_h, \mu_v, \sigma_h, \mbox{and } \sigma_v\)) rather than the experimentally determined factors (i.e. \(\bar{h}, \bar{v}, s_h, \mbox{and } s_v\)) on purpose to emphasize the theoretical nature of the assumptions. Of course the "true" population parameters are unknown, and they could only be estimated with the corresponding experimentally fitted values about which there is some error.

Conformance Testing

\(\rho \approx 0\)

only way linear least squares

\(\sigma_h \approx \sigma_v \)

  1. F-Test \(\frac{s_h^2}{s_v^2}\)     if    \(s_h < s_v\)    else    \(\frac{s_v^2}{s_h^2}\)
  2. Studentized Ranges
  3. Chi-Squared \((n-1) \frac{s^2}{\hat{\sigma}^2}\)

Circular Shot Distribution about COI

Case 1, Rayleigh Distribution

Shots dispersed about the COI. A circular dispersion is the Rayleigh distribution.

Given:

  1. \(\sigma_h \approx \sigma_v\)
  2. \(\rho \approx 0\)

then the mathematical formula for the dispersion distribution would be the Rayleigh distribution:
    \(f(r) = \frac{r}{\Re^2} e^{-r^2/(2\Re^2)}, \quad r \geq 0,\) and \(\Re\) is the shape factor of the Rayleigh distribution.

This is really the best case for shot dispersion. Shot groups would be round.

Strictly, for the Rayleigh distribution to apply, then \(\sigma_h = \sigma_v\), in which case \(\Re = \sigma_h = \sigma_v\). For the "loose" application of the Rayleigh distribution to apply, then \(\Re \approx (\sigma_h + \sigma_v)/2 \approx \sqrt{\frac{\sigma_h^2 + \sigma_v^2}{2}}\).

The following statistical measurements are appropriate:

  • Circular Error Probable (CEP)
  • Covering Circle Radius (CCR)
  • Diagonal
  • Extreme Spread (ES)
  • Figure of Merit (FOM)
  • Mean Radius (MR)
  • Radial Standard deviation

Notes:

  1. The Diagonal, the Extreme Spread and the FOM are different measurements, even though they conceivable could be based on the same two shots! The Extreme Spread would only depend on the two shots most distant in separation. The the Diagonal and the FOM would depend on two to four shots. For a large number of shots we'd typically expect four different shots to define the extremes for horizontal and vertical deflection.
  2. For the measures for the CCR, the Diagonal, the GS and the FOM measurements a target would a ragged hole would be acceptable, but for the rest of the measures the {h,v} positions of each shot must be known.
  3. Experimentally the radial distance for each shot, i, is \(r_i = \sqrt{(h_i - \bar{h})^2 + (v_i - \bar{v})^2}\)
  4. The conversion to polar coordinates results in each shot having coordinates \((r, \theta)\). (a) The conversion implicitly assumes that the polar coordinates have been translated so that the center is at the Cartesian Coordinate of the true center of the population \((\bar{h}, \bar{v})\). (b) The distribution of \(\theta\) is assumed to be entirely random and hence irrelevant. This assumption is testable. (c) The distribution is thus converted from a two-variable distribution to a one-variable distribution.
Bullseye.jpg Note that there is a conundrum in how we are "averaging" the horizontal and vertical standard deviations to get \(\sigma_{\Re}\). Look at the two expressions. They lead to two choices, either of which may casually seem valid.
  • \(\sigma_h = \sigma_v\)
  • \(\sigma_h^2 = \sigma_v^2\)

In general if we look at the first formula "averaging" it leads to using:

   \(\Re = \frac{\sigma_h + \sigma_v}{2} = \sigma_h\)   (with substituting \(\sigma_h\) for \(\sigma_v\))

However in statistics standard deviations are "averaged" (pooled) by taking the square root of the average of their variances:
   \(\Re^2 = {\frac{\sigma_h^2 + \sigma_v^2}{2}}\)
   \(\Re = \sqrt{\frac{\sigma_h^2 + \sigma_v^2}{2}} = \sigma_h \)  (with substituting \(\sigma_h\) for \(\sigma_v\))

but:

   \(\frac{\sigma_h + \sigma_v}{2} = \sqrt{\frac{\sigma_h^2 + \sigma_v^2}{2}}\)   if and only if \(\sigma_h \equiv \sigma_v\)

Thus we should take the extent that:

   \(\frac{\sigma_h + \sigma_v}{2} \neq \sqrt{\frac{\sigma_h^2 + \sigma_v^2}{2}}\)

as a severe warning that we can not push the assumption that \(\sigma_h \approx \sigma_v\) too far if we expect the simplification of the general Hoyt distribution to the Rayleigh distribution to give meaningful results.

The situation is even more tenuous given the small samples that shooters typically use. In general the relative precision of the variance value about a mean is much less precise than the relative precision of the mean value. The statistical test to compare two experimental variance values (i.e. \(\sigma_h^2, \text{and} \sigma_v^2\) in our case) is the F-Test which uses the ratios of the variances. For small samples a large difference would need to be observed before the ratio would be statistically significantly because of the imprecision in the individual experimental variance values.

Elliptical Shot Distribution about COI

Case 2, Equal variances and correlated

Given:

  1. \(\sigma_h \approx \sigma_v\)
  2. \(\rho \neq 0\)
  3. The {h,v} position of each shot must be known.

The following statistical measurement is appropriate:

  • Elliptic Error Probable

Case 3, Unequal variances and uncorrelated (Orthogonal Elliptical Distribution)

Given:

  1. \(\sigma_h \neq \sigma_v\)
  2. \(\rho \approx 0\)
  3. The {h,v} position of each shot must be known.

then the mathematical formula for the dispersion distribution would be:
    \( f(h,v) = \frac{1}{2 \pi \sigma_h \sigma_v} \exp\left( -\frac{1}{2}\left[ \frac{h^2}{\sigma_h^2} + \frac{v^2}{\sigma_v^2} \right] \right) \) For the purposes of this wiki, this distribution will be called the Orthogonal Elliptical Distribution. It is obviously a special case of the Hoyt distribution which in turn is a special case of the bivariate normal distribution.

In order of the model complexity, the following statistical measurements are appropriate:

  • Individual Horizontal and Vertical variances
  • Elliptic Error Probable

In this case the horizontal and vertical standard deviations could be determined independently from the horizontal and vertical measurements respectively.

Case 4, Unequal variances and correlated (Hoyt Distribution)

Hoyt Distribution - Shots dispersed about COI in an elliptical pattern which has its major axis at an angle to the coordinate axes.

Given:

  1. \(\sigma_h \neq \sigma_v\)
  2. \(\rho \neq 0\)
  3. The {h,v} position of each shot must be known.

then the mathematical formula for the dispersion distribution would be the Hoyt distribution with no simplifications:
    \( f(h,v) = \frac{1}{2 \pi \sigma_h \sigma_v \sqrt{1-\rho^2}} \exp\left( -\frac{1}{2(1-\rho^2)}\left[ \frac{h^2}{\sigma_h^2} + \frac{v^2}{\sigma_v^2} - \frac{2\rho h v}{\sigma_h \sigma_v} \right] \right) \)

Shot groups would be elliptical or egg-shaped if either the horizontal range or vertical range were large. The following statistical measurements are appropriate:

  • Elliptic Error Probable

Related topics

See also the following topics which are closely related:

  • Error Propagation - A basic discussion of how errors propagate when making measurements.
  • Stringing - Definition of stringing and how it can be handled

References



Next: Precision Models

Retrieved from "http://ballistipedia.com/index.php?title=Projectile_Dispersion_Classifications&oldid=1270"