Projectile Dispersion Classifications

Dispersion Classifications

Before considering the measurements that will be used for the actual statistical analysis, let's consider the assumptions about dispersion and how sets of those assumptions might be grouped into different classifications. Thus the various classifications will offer insight as to the fundamental patterns expected for shots and insights to the interactions of various measures. Thus an understanding of the basic assumptions about dispersion is key in being able to effectively use the measures.

In order to discuss dispersion we are going to neglect all of the factors of internal and external ballistics that cause a bias to the Center of Impact (COI) on a target. For example, even though we know that gravity will make a projectile's path drop over its time of flight, we are ignoring the fact that the boreline must be elevated. The overall error that we are interested in measuring is the sum of all the various interactions that make multiple projectiles shot to the same point of aim (POA) disperse about the COI.

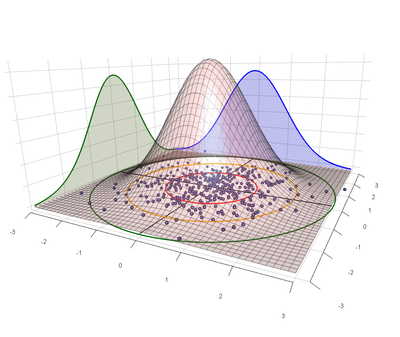
The Normal distribution is the broadly assumed probability model used for a single random variable and it is characterized by its mean \((\bar{x})\) and standard deviation \((\sigma)\). The central limit theorem shows that for measures for the "average" shot, or averages of multiple targets are used, then for "large" samples the averages will conform to Normal distribution even if the fundamental distribution is not a normal distribution.

Distribution of samples from a symmetric bivariate normal distribution. Axis units are multiples of σ.

Since we are interested in shot dispersion on a two-dimensional target we will assume that the horizontal and vertical dispersions are each Normal distributions. Thus the horizontal dispersion will have mean \(\mu_h\) and standard deviation \(\sigma_h\). The vertical dispersion will have mean \(\mu_v\) and standard deviation \(\sigma_v\). Then a further assumption is made by assuming that the two dimensional expansion of the Normal distribution the Bivariate Normal distribution, applies. This adds an additional term the correlation parameter ρ. Thus the expectation is that distribution should then describe, the dispersion of a gunshots about the COI, (\(\mu_h\) and \(\mu_v\)). The full bivariate normal distribution is thus:
    \( f(h,v; \mu_h, \mu_v, \sigma_h, \sigma_v, \rho) = \frac{1}{2 \pi \sigma_h \sigma_v \sqrt{1-\rho^2}} \exp\left( -\frac{1}{2(1-\rho^2)}\left[ \frac{(h-\mu_h)^2}{\sigma_h^2} + \frac{(v-\mu_v)^2}{\sigma_v^2} - \frac{2\rho(h-\mu_h)(v-\mu_v)}{\sigma_h \sigma_v} \right] \right) \)

where:
    \(-1 ≤ \rho ≤ 1\)
    \( \sigma_h>0 \) and \( \sigma_v>0 \)

Note that the above restrictions are not additional restrictions on the model, but rather simply pointing out how the mathematics works. Rather they are more analogous to the fact that a person can't have a negative age (even if they act like it...).

Since we are primarily interested in the dispersion relative to the COI, the overall assumption is that the weapon could be properly sighted so that the center of impact would be the same as the point of aim. In practice this is achieved by adjusting the weapon's sights.

An ancillary point worth mentioning is that the assuming the Normal distribution in three dimensions leads to the Maxwell–Boltzmann distribution which is the foundation of the ideal gas laws.

Simplifications into cases

To eliminate the sighting variables (\(\bar{h}\) and \(\bar{v}\)) which make the equations "messier", a translation of the coordinate system to the COI (\(\bar{h}\),\(\bar{v}\)) is assumed. This is a very pragmatic and justifiable consideration since the COI can be measured on the target. This simplification of the dispersion equations is strictly for easy of understanding as is not a limitation on any of the dispersion classifications. With the translation of the coordinate system to the COI, then the general bivariate normal equation becomes the Hoyt distribution:
    \( f(h,v; \sigma_h, \sigma_v, \rho) = \frac{1}{2 \pi \sigma_h \sigma_v \sqrt{1-\rho^2}} \exp\left( -\frac{1}{2(1-\rho^2)}\left[ \frac{h^2}{\sigma_h^2} + \frac{v^2}{\sigma_v^2} - \frac{2\rho hv}{\sigma_h \sigma_v} \right] \right) \)

Looking at this equation two other different mutually exclusive simplifications can be readily seen:

• Either \(\sigma_h = \sigma_v\) (equal standard deviations) or \(\sigma_h \neq \sigma_v\) (unequal standard deviations).

Obviously if we could measure both \(\sigma_h\) and \(\sigma_v\) with a very high precision (e.g 6 significant figures), then the two quantities would never really be equal. But in many cases the assumption is reasonable. In reality since shooters typically collect only a small amount of data, statistical tests will fail to detect a difference unless the difference is great. In such cases the shot pattern would be noticeably elliptical, not round.

• Either \(\rho = 0\) (uncorrelated) or \(\rho \neq 0\) (correlated).

: !! CAREFUL !! Correlation does not imply causation

There is somewhat famous example. A researcher gathered statistics for stork sightings and births in a particular county over a twenty year period. Analysis of the data showed that over the twenty year period both stork sightings and births had increased with a very significant linear correlation. From the data you might erroneously infer that storks do bring babies!

The pair of mutually exclusive assumptions thus results in four cases for analytical evaluation as shown in the Table below. There is one case that results in circular groups, and three that result in elliptical groups. As the different in variances gets greater, or the further \(\rho\) is from 0, then the ellipse will be more pronounced.

Group Shape vs. Assumptions

	\(\sigma_h \approx \sigma_v\)	\(\sigma_h \neq \sigma_v\)
\(\rho \approx 0\)	Case 1 - Circular Groups special case is Rayleigh Distribution	Case 3 - Elliptical Groups Major axis of ellipse along horizontal or vertical axis
\(\rho \neq 0\) Major axis of ellipse at an angle to both the horizontal and vertical axes	Case 2- Elliptical Groups	Case 4 - Elliptical Groups general case of Hoyt distribution required

The table above uses approximately equal to \((\approx)\)) rather than strictly equal to (=). This is an acknowledgement that we are dividing the cases into ones that are close enough to be useful, even though they most certainly are not exact. To be overly persnickety there are two considerations.

First we can only get experimental estimates from calculations based on sample data for the factors \(\sigma_h\), \(\sigma_v\), \(\rho\) and these estimates are at best only good to a scant few significant figures. Thus even though the difference between approximately equal to and strictly equal to is under some experimental control there are practical limits. In other words, we can theoretically make the measurements as precise as we want by collecting more data, but it is quickly impractical to do so. (Assume that to double the precision that we have to quadruple the sample size. This exponential increase quickly becomes unmanageable. It is easy to pontificate about averaging over a million targets, but no one is going to shoot that many.) Thus even if \(\sigma_h \equiv \sigma_v\) we'd never expect that we'd experimentally get \(s_h = s_v\) due to experimental error.

Second there is the good enough. Shooting by definition is going to have fairly small sample sizes. So if \(0.66s_h < s_v < 1.5 s_h\) then, as a rule of thumb, that is probably good enough. Of course for large sample we would want to tighten the window.

The formulas for the distributions in the sections below are given in terms of the population parameters (i.e. \(\mu_h, \mu_v, \sigma_h, \mbox{and } \sigma_v\)) rather than the experimentally determined factors (i.e. \(\bar{h}, \bar{v}, s_h, \mbox{and } s_v\)) on purpose to emphasize the theoretical nature of the assumptions. Of course the "true" population parameters are unknown, and we estimate them with the corresponding experimentally fitted values about which there is some error.

Conformance Testing

\(\rho \approx 0\)

only way linear least squares

\(\sigma_h \approx \sigma_v \)

1. F-Test \(\frac{s_h^2}{s_v^2}\)     if    \(s_h < s_v\)    else    \(\frac{s_v^2}{s_h^2}\)
2. Studentized Ranges
3. Chi-Squared \((n-1) \frac{s^2}{\hat{\sigma}^2}\)

Circular Shot Distribution

Case 1, Rayleigh Distribution

Given:

1. \(\sigma_h \approx \sigma_v\)
   
2. \(\rho \approx 0\)
   

then the mathematical formula for the dispersion distribution would be the Rayleigh distribution:
    \(f(r) = \frac{r}{\sigma_{\Re}^2} e^{-r^2/(2\sigma_{\Re}^2)}, \quad r \geq 0,\) and \(\sigma_{\Re}\) is the distribution shape factor known as the Radial Standard Deviation.

This is really the best case for shot dispersion. Shot groups would be round.

Strictly, for the Rayleigh distribution to apply, then \(\sigma_h = \sigma_v\), in which case \(\sigma_{\Re} = \sigma_h = \sigma_v\). For the "loose" application of the Rayleigh distribution to apply, then \(\sigma_{\Re} \approx (\sigma_h + \sigma_v)/2\).

Note that there is a conundrum in how we are "averaging" the horizontal and vertical axes. Look at the two expressions. They lead to two choices, either of which may casually seem valid. \(\sigma_h = \sigma_v\) \(\sigma_h^2 = \sigma_v^2\) In general if we look at the first formula "averaging" it leads to using:    \(\sigma_{\Re} = \frac{\sigma_h + \sigma_v}{2} = \sigma_h\)   (with substituting \(\sigma_h\) for \(\sigma_v\)) However in statistics standard deviations are "averaged" (pooled) by taking the square root of the variances:    \(\sigma_{\Re} = \sqrt{\sigma_h^2 + \sigma_v^2} = \sigma_h \sqrt{2}\)  (with substituting \(\sigma_h\) for \(\sigma_v\)) We could "fix" the second method by using a correction factor as:    \(\sigma_{\Re} = \frac{\sqrt{\sigma_h^2 + \sigma_v^2}}{\sqrt{2}}\) but:    \(\frac{\sigma_h + \sigma_v}{2} = \frac{\sqrt{\sigma_h^2 + \sigma_v^2}}{\sqrt{2}}\)   if and only if \(\sigma_h \equiv \sigma_v\) Thus we should take the extent that:    \(\frac{\sigma_h + \sigma_v}{2} \neq \frac{\sqrt{\sigma_h^2 + \sigma_v^2}}{\sqrt{2}}\) as a severe warning that we can not push \(\sigma_h \approx \sigma_v\) too far if we expect the simplification of the general Hoyt distribution to the Rayleigh distribution to give meaningful results.

The following statistical measurements are appropriate:

• Circular Error Probable (CEP)
• Covering Circle Radius (CCR)
• Diagonal
• Extreme Spread (ES)
• Figure of Merit (FOM)
• Mean Radius (MR)
• Rayleigh Distribution

Notes:

1. The Diagonal, the Extreme Spread and the FOM are different measurements, even though they conceivable could be based on the same two shots! The Extreme Spread would only depend on the two shots most distant in separation. The the Diagonal and the FOM would depend on two to four shots. For a large number of shots we'd typically expect four different shots to define the extremes for horizontal and vertical deflection.
2. For the measures for the CCR, the Diagonal, the GS and the FOM measurements a target would a ragged hole would be acceptable, but for the rest of the measures the {h,v} positions of each shot must be known.
3. Experimentally the radial distance for each shot, i, is \(r_i = \sqrt{(h_i - \mu_h)^2 + (v_i - \mu_v)^2}\)
4. The conversion to polar coordinates results in each shot having coordinates \((r, \theta)\). (a) The conversion implicitly assumes that the polar coordinates have been translated so that the center is at the Cartesian Coordinate of the true center of the population \((\bar{h}, \bar{v})\). (b) The distribution of \(\theta\) is assumed to be entirely random and hence irrelevant. This assumption is testable. (c) The distribution is thus converted from a two-variable distribution to a one-variable distribution.

Elliptical Shot Distribution

Case 2, Equal variances and correlated

Given:

1. \(\sigma_h \approx \sigma_v\)
   
2. \(\rho \neq 0\)
   
3. The {h,v} position of each shot must be known.

The following statistical measurement is appropriate:

• Elliptic Error Probable

Case 3, Unequal variances and uncorrelated

Given:

1. \(\sigma_h \neq \sigma_v\)
   
2. \(\rho \approx 0\)
   
3. The {h,v} position of each shot must be known.

then the mathematical formula for the dispersion distribution would be:
    \( f(h,v) = \frac{1}{2 \pi \sigma_h \sigma_v} \exp\left( -\frac{1}{2}\left[ \frac{h^2}{\sigma_h^2} + \frac{v^2}{\sigma_v^2} \right] \right) \)

• Elliptic Error Probable

The following statistical measurements are appropriate:

• Individual Horizontal and Vertical variances

In this case the horizontal and vertical standard deviations could be determined independently from the horizontal and vertical measurements respectively.

Case 4, Unequal variances and correlated (Hoyt Distribution)

Given:

1. \(\sigma_h \neq \sigma_v\)
   
2. \(\rho \neq 0\)
   
3. The {h,v} position of each shot must be known.

then the mathematical formula for the dispersion distribution would be the Hoyt distribution with no simplifications:
    \( f(h,v) = \frac{1}{2 \pi \sigma_h \sigma_v \sqrt{1-\rho^2}} \exp\left( -\frac{1}{2(1-\rho^2)}\left[ \frac{h^2}{\sigma_h^2} + \frac{v^2}{\sigma_v^2} - \frac{2\rho h v}{\sigma_h \sigma_v} \right] \right) \)

Shot groups would be elliptical or egg-shaped if either the horizontal range or vertical range were large.

Related topics

See also the following topics which are closely related:

• Error Propagation - A basic discussion of how errors propagate when making measurements.
• Stringing - Definition of stringing and how it can be handled

References

---

Next: Precision Models