Closed Form Precision
Previous: Measuring Precision
Contents
The Precision Parameter
Measuring Precision showed how a single parameter σ (sigma) characterizes the precision of a shooting system.
This σ is the parameter for the Rayleigh distribution with probability density function \(\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}\). The associated Cumulative Distribution Function gives us the probability that a shot falls within a given radius of the center:
- \(Pr(r \leq \alpha) = 1 - e^{-\alpha^2 / 2 \sigma}\)
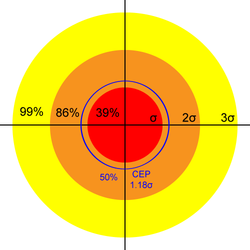
Therefore, we expect 39% of shots to fall within a circle of radius σ, 86% within 2σ, and 99% within 3σ.
Using the characteristics of the Rayleigh distribution we can immediately compute the three most useful precision measures:
Mean Radius (MR)
Mean Radius \(MR = \sigma \sqrt{\frac{\pi}{2}} \ \approx 1.25 \ \sigma\).
\(1 - e^{-\frac{\pi}{4}} \approx 54\%\) of shots should fall within the mean radius. 96% of shots should fall within the mean diameter (MD = 2 MR).
The expected sample MR of a group of size n is
- \(MR_n = \sigma \sqrt{\frac{\pi}{2 c_{B}(n)}}\ = \sigma \sqrt{\frac{\pi (n - 1)}{2 n}}\)
(This sample size adjustment doesn't use the Gaussian correction factor because the mean radius is not an estimator for σ, even though in the limit the true value of one is a constant product of the other.)
Radial Standard Deviation (RSD)
Radial Standard Deviation \(RSD = \sigma \sqrt{\frac{4 - \pi}{2}} \ \approx 0.66 \ \sigma\).
\(1 - e^{-\frac{4-\pi}{4}} \approx 19\%\) of shots should fall within a radial standard deviation of the center.
The expected sample RSD of a group of size n is
- \(RSD_n = \sigma \sqrt{\frac{4-\pi}{2 c_{B}(n)}}\)
Circular Error Probable (CEP)
Circular Error Probable \(CEP = \sigma \sqrt{\ln(4)} \ \approx 1.18 \ \sigma\). 50% of shots should fall within the circular error probable.
In theory CEP is the median radius, but especially for small n the sample median is a very bad estimator for true median. Nevertheless, if you want to know the expected sample median radius of a group of size n it turns out the following is a good estimate:
- \(CEP_n = \sigma \frac{\sqrt{\ln(4)}}{c_{G}(n) c_{R}(n)}\)
Summary Sigma Probabilities
| Name | Radius in Sigmas | Shots Covered |
|---|---|---|
| RSD | 0.66 | 19% |
| 1 | 39% | |
| CEP | 1.18 | 50% |
| MR | 1.25 | 54% |
| 2 | 86% | |
| MD | 2.5 | 96% |
| 3 | 99% |
Typical values of σ
A lower bound on σ is probably that displayed by rail guns in 100-yard competition. On average they can place 10 rounds into a quarter-inch group, which as we will see shortly suggests σ = 0.070MOA, or under 0.025mil.
The U.S. Precision Sniper Rifle specification requires a statistically significant number of 10-round groups fall under 1MOA. This means σ = 0.28MOA, or under 0.1mil.
The specification for the M110 semi-automatic sniper rifle (MIL-PRF-32316) as well as the M24 sniper rifle (MIL-R-71126) requires MR below 0.65SMOA, which means σ = 0.5MOA. The latter spec indicates that an M24 barrel is not considered worn out until MR exceeds 1.2MOA, or σ = 1MOA!
XM193 ammunition specifications require 10-round groups to fall under 2MOA. This means σ = 0.6MOA or 0.2mil, and it is a good minimum precision standard for light rifles.
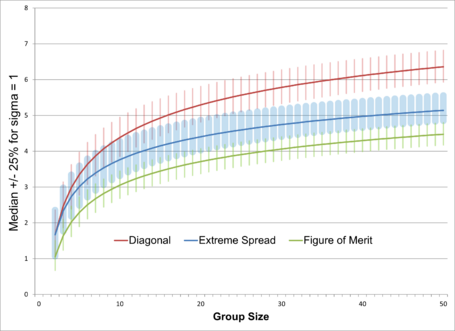
Spread Measures
The three measures that vary with n (Extreme Spread, Diagonal, and Figure of Merit) are range statistics that lack convenient functional forms. However both the mean and standard deviation of their expected value, as well as quantiles, scale directly with σ, so it is sufficient to calculate those statistics once for σ = 1 and multiply the resulting values by the desired σ. Media:Sigma1RangeStatistics.xls contains quantiles and moments for n up to 100.
Example 1
What extreme spread should I expect for 5-shot groups from my rifle? The extreme spread median from the table for 5 shots is 3.0 σ. I've determined my rifle has precision σ = ½MOA. If I take five shots at 100 yards we would expect half my groups to be less than 3.0/2 = 1.5MOA \(\approx\) 1.6".
Multiplying the rest of the distribution data for that row by my 0.5MOA we can also say that the extreme spread of my 5-shot groups should exhibit the following distributions:
- 50% between (1.2, 1.8)MOA
- 80% between (1.0, 2.1)MOA
- 95% between (0.8, 2.4)MOA
Example 2
Over many tests I have found my rifle produces 5-shot groups with an average extreme spread of 1MOA. What extreme spread should I expect if I instead start shooting 10-shot groups? The table shows that the ratio of expected extreme spreads on 10-shot groups is 1.24 times the value on 5-shot groups. So my a priori expectation would be for 10-shot groups to average 1.24MOA.
Example 3
How meaningful is a 3-shot precision guarantee? The first answer is that any performance standard that is expressed in terms of group sizes is probably meaningless. After all, even the most precise gun will occasionally shoot a wide 3-shot group, and a shot-out barrel will with some probability still put three rounds through the same hole. The inherent precision of a gun is revealed over a large number of shots, and it doesn't matter how those shots are sampled: neither the gun nor the target has a memory. If we shoot 100 rounds through a rifle, we could pick any three at random as a 3-shot group. Therefore, a precision guarantee has to hold over a large number of shots and is more aptly expressed in terms of probabilities. E.g., "99% of shots with our rifle will fall within a ½MOA radius." Based on the Rayleigh CDF this 99% claim is the same as saying 3σ = ½MOA, or that the rifle's precision σ = 1/6MOA.
There are two qualifications to the preceding:
- We do know that the sample size of a 3-shot group is smaller than the sample size of larger groups, simply because the sample center is closer to the sample shots than the true center. This is shown in the correction terms above. For example, the average 3-shot group has a mean radius \(1/\sqrt{c_B(3)} \approx 80\%\) the size of the mean radius measured from twenty or more shots.
- It is not exactly true that guns have no memory: The effects of heating and fouling can create second-order changes in both the precision and point of impact. So it might be necessary to qualify a precision guarantee with limits on barrel temperature and/or prescriptions on how many shots be fired between bore cleaning. And in the limit barrels erode and have a finite lifespan, so especially with higher-power calibers practical limits do exist on how long precision can stay constant.
Next: Examples